Структура смешанного состояния сверхпроводников II-го рода.
В сверхпроводниках II-го рода образование границ сверхпроводника и нормального состояния – выгодно, так как
Можно показать, что вихри отталкиваются друг от друга, т.е. их энергия взаимодействия положительна и они стремятся расположиться как можно дальше друг от друга (физически это, фактически, следует из закона Бернулли: в пространстве между вихрями соответствующие им скорости потока вычитаются, и следовательно, давление увеличивается). Максимальному расстоянию между вихрями при их фиксированной концентрации отвечает их расположение в узлах треугольной решетки. Семинар 8-9. Эффект Джозефсона и его применения. Стационарный эффект Джозефсона. Нестационарный эффект Джозефсона. СКВИДы и их использование для магнитных измерений. Влияние магнитного поля на джозефсоновский переход. ВАХ джозефсоновского перехода. Уравнение для фазы с учетом диссипации и механическая аналогия. Физическая природа гистерезиса ВАХ. Нестационарный эффект Джозефсона. Макроскопические квантовые эффекты в джозефсоновских переходах. Пусть имеется два сверхпроводника, разделенные тонкой, туннельно-прозрачной пленкой диэлектрика.
Согласно второму уравнению Гинзбурга-Ландау в объеме сверхпроводника
Вид граничных условий к уравнению Гинзбурга-Ландау для сверхпроводников, находящихся в туннельном контакте, можно установить из следующих общих рассуждений. Мысленно разрежем туннельный контакт и разнесем сверхпроводники друг от друга. На образовавшейся поверхности граничные условия будут иметь стандартный для свободной поверхности вид:
При восстановлении контакта вид граничного условия в рассматриваемом сверхпроводнике должен измениться таким образом, чтобы учесть присутствие другого сверхпроводника. Это влияние можно описать, добавив в правую часть граничного условия функцию f(Ψi)=ηΨi, линейно зависящую от параметра порядка соседнего сверхпроводника (свободной поверхности отвечает равенство нулю этого параметра порядка и функции f):
С учетом полученных граничных условий градиентные члены в выражении для сверхпроводящего тока (2-м уравнении Гинзбурга-Ландау) преобразуются следующим образом
Считая параметр η действительным получим следующее выражение для сверхпроводящего тока
Которое можно переписать в стандартном виде, описывающим стационарный эффект Джозефсона:
где Нестационарный эффект Джозефсона Рассмотрим ситуацию, когда на переходе имеется разность потенциалов.
Уравнение, связывающее фазу и напряжение можно получить из условий калибровочной инвариантности. Калибровочная инвариантность означает инвариантность физически наблюдаемых величин при калибровочном преобразовании
Наша цель будет заключаться в том, чтобы найти такое соотношение, связывающее фазу и напряжение, которое оставалось бы инвариантным при таком преобразовании. Калибровочное преобразование очевидным образом оставляет инвариантным магнитное поле
и уравнение Максвелла
где напряженность электрического поля определяется через вектор-потенциал и скалярный (электрический) потенциал
Из требования инвариантности напряженности электрического поля следует правило калибровочного преобразования электрического потенциала
Таким образом для напряжения (разности потенциалов) получаем следующую формулу преобразования:
Как следует из 1-го уравнения Гинзбурга-Ландау фаза параметра порядка θ меняется следующим образом:
что оставляет инвариантным градиентный член в уравнении Гинзбурга-Ландау
В результате для разности фаз на джозефсоновском переходе получаем следующее выражение:
Сопоставив это выражение с выражением для напряжения, получим следующее соотношение связывающее разность фаз и напряжение на джозефсоновском переходе:
или
Данное выражение уже остается инвариантным при калибровочном преобразовании. Пусть к туннельному переходу приложено постоянное напряжения. Из полученного соотношения находим следующее выражение для разности фаз
Подставив его в формулу для джозефсоновского тока, получим следующее выражение, описывающее нестационарный эффект Джозефсона
Суть нестационарного эффекта Джозефсона в том, что в туннельном контакте двух сверхпроводников, к которому приложено напряжение V, возможны электромагнитные колебания с частотой
Физическая природа джозефсоновских колебаний становится более понятной, если учесть, что в сверхпроводящем состоянии электроны образуют пары (куперовские пары) с зарядом 2е. При переходе через туннельный контакт, к которому приложено напряжение V, куперовская пара приобретает дополнительную энергию 2eV, которая выделяется в виде кванта электромагнитного излучения с энергией Эффект Джозефсона представляет собой яркое физическое явление, имеющее важное фундаментальное и прикладное значение. За его предсказание английскому физику Б.Джозефсону в 1973 г. была присуждена Нобелевская премия. Заметим, что для существования эффектов Джозефсона необязательно наличие туннельной прослойки. Эффект сохраняется в более широком классе контактов, характеризующихся наличием «слабой связи» - небольшой области, в которой сверхпроводимость подавлена, например, микросужения.
Сверхпроводниковый квантовый интерферометр Джозефсона (СКВИД) СКВИД (на английском – SQUID – Superonducting QUantum Interference Device) – сверхчувствительный магнетометр, один из наиболее распространенных сверхпроводниковых приборов. Рассмотрим, так называемый, двухплечевой СКВИД, представляющий собой сверхпроводящую петлю с входным и выходным токовыми контактами, в которую вставлены два джозефсоновских перехода (контакта) a и b.
Подобно тому, как мы это делали при выводе формулы для квантования магнитного потока в сверхпроводящей полости, рассмотрим разрывный контур C`, который находится в объеме материала сверхпроводящего кольца на расстоянии от поверхности большем, чем глубина проникновения магнитного поля, и имеет точки разрыва на берегах туннельных контактов толщиной δ. Ток на контуре, при этом равен нулю. На туннельных контактах фаза испытывает скачки и член с градиентом фазы в выражении для тока не определен:
Проинтегрируем на контуре C` выражение для тока. Поскольку вектор-потенциал – гладкая функция и длина δ разрыва контура мала, в интеграле для вектор-потенциала контур C` можно дополнить да замкнутого контура С
расписывая интеграл для градиента фазы по разрывному контуру получаем:
или
Запишем выражение для полного тока:
Полученное выражение можно переписать в виде аналогичном формуле для стационарного эффекта Джозефсона в одиночном туннельном контакте:
Таким образом мы получили, что максимальное значение сквозного тока через СКВИД существенно зависит от величины магнитного потока через площадь, охватываемую сверхпроводящей петлей. При
|

 , однако дробление нормальной области с
, однако дробление нормальной области с  ограничивает условие квантования магнитного потока. Таким образом, магнитное поле проникает в сверхпроводники II-го рода в виде вихрей (вихрей Абрикосова), представляющих из себя сердцевину, вокруг которой циркулируют сверхпроводящие токи, экранирующие магнитное поле центра вихря в объеме сверхпроводника. Полный поток магнитного поля, связанный с вихрем, равен одному кванту потока.
ограничивает условие квантования магнитного потока. Таким образом, магнитное поле проникает в сверхпроводники II-го рода в виде вихрей (вихрей Абрикосова), представляющих из себя сердцевину, вокруг которой циркулируют сверхпроводящие токи, экранирующие магнитное поле центра вихря в объеме сверхпроводника. Полный поток магнитного поля, связанный с вихрем, равен одному кванту потока.

 , т. е. ток связан с изменением фазы параметра порядка. Поэтому можно ожидать, что и в туннельном контакте двух сверхпроводников, в случае возникновения скачка фазы должен будет возникнуть ток, равный нулю в отсутствие скачка фазы:
, т. е. ток связан с изменением фазы параметра порядка. Поэтому можно ожидать, что и в туннельном контакте двух сверхпроводников, в случае возникновения скачка фазы должен будет возникнуть ток, равный нулю в отсутствие скачка фазы:



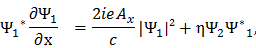

 ,
, - максимальное значение амплитуды тока, который может протекать через туннельный контакт двух сверхпроводников в отсутствие приложенного напряжения. Необычность ситуации связана с тем, что бездиссипативный ток протекает через структуру, содержащую несверхпроводящую туннельную прослойку. Туннельный контакт двух сверхпроводников иначе называют джозефсоновским контактом.
- максимальное значение амплитуды тока, который может протекать через туннельный контакт двух сверхпроводников в отсутствие приложенного напряжения. Необычность ситуации связана с тем, что бездиссипативный ток протекает через структуру, содержащую несверхпроводящую туннельную прослойку. Туннельный контакт двух сверхпроводников иначе называют джозефсоновским контактом.







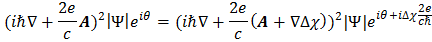

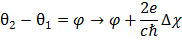


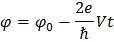


 .
.


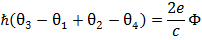
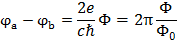

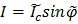

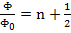 максимальный ток равен нулю
максимальный ток равен нулю 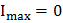 , сверхпроводящее состояние неустойчиво и СКВИД переходит в состояние с конечной проводимостью. Величина потока зависит от площади кольца, что, в силу малости кванта потока позволяет регистрировать очень маленькие магнитные поля. На практике обычно регистрируют изменения магнитного поля, при этом чувствительность СКВИДов достигает величины
, сверхпроводящее состояние неустойчиво и СКВИД переходит в состояние с конечной проводимостью. Величина потока зависит от площади кольца, что, в силу малости кванта потока позволяет регистрировать очень маленькие магнитные поля. На практике обычно регистрируют изменения магнитного поля, при этом чувствительность СКВИДов достигает величины  (напомним, что напряженность магнитного поля Земли
(напомним, что напряженность магнитного поля Земли 




