Стандарт напряжения.Одно из наиболее важных, наряду со сквидами, приложений сверхпроводников в аналоговой электронике представляют собой стандарты напряжения. Из выражения для тока в нестационарном эффекте Джозефсона при постоянном напряжении на переходе следует, что среднее значение тока по времени равно нулю. Рассмотрим ситуацию, когда на джозфсоновском переходе присутствует как постоянное напряжение V0, так и переменное напряжение V1(t)=-V1cos(ωt). Решив уравнение для фазы
Можно показать, что среднее значение этого тока по времени уже не равно нулю. Выполним разложение функции «синус от синуса» в ряд по функциям Бесселя целого порядка Jn:
Как нетрудно видеть при
среднее значение тока отлично от нуля и равно
В эксперименте измеряется именно среднее значение тока. Поэтому при наличии на джозефсоновском переходе одновременно постоянного V0 и переменного смещения V1(t) данный эффект будет проявлять себя в возникновении на вольт-амперной характеристике перехода ступенек тока на фоне зависимости
Такие ступеньки называют ступеньками Шапиро. Величина скачка тока зависит от амплитуды переменного напряжения и других параметров, но само положение скачка на оси V0 определяется только частотой и мировыми постоянными. Поскольку для определения частоты имеются высокоточные стандарты, данный эффект можно использовать для определения напряжения с высокой точностью и создания стандарта напряжения.
|
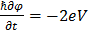, получим выражение для джозефсоновского тока: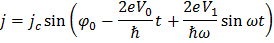
.
.
:
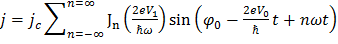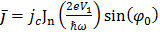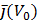