Непараметрические методы
Применение корреляционного и регрессионного анализа требует, чтобы все признаки были количественно измеренными. Построение аналитических группировок предполагает, что количественным должен быть результативный признак. Параметрические методы основаны на использовании основных количественных параметров распределения (средних величин и дисперсий). Вместе с тем в статистике применяются также непараметрические методы, с помощью которых устанавливается связь между качественными (атрибутивными) признаками. Сфера их применения шире, чем параметрических, поскольку не требуется соблюдения условия нормальности распределения зависимой переменной, однако при этом снижается глубина исследования связей. При изучении зависимости между качественными признаками не ставится задача представления ее уравнением. Здесь речь идет только об установлении наличия связи и измерении ее тесноты. В практике статистических исследований приходится иногда анализировать связи между альтернативными признаками, представленными только группами с противоположными (взаимоисключающими) характеристиками. Тесноту связи в этом случае можно оценить, вычислив коэффициенты ассоциации и контингенции. Коэффициент ассоциации определяется по формуле
Коэффициент контингенции определяется по формуле
где a, b,c,d - частоты (число единиц). Для расчета коэффициентов ассоциации и контингенции строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т.е. состоящим из двух качественно отличных друг от друга значений признака.
Коэффициенты ассоциации и контингенции изменяются от —1 до +1; чем ближе к +1 или -1, тем сильнее связаны между собой изучаемые признаки. Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной,если К,>0,5 или К,>0,3. Если по каждому из взаимосвязанных признаков выделяется число групп более двух, то для подобного рода таблиц теснота связи между качественными признаками может быть измерена с помощью показателей взаимной сопряженности Пирсона.
где Вычтя из этой суммы единицу, получим Вспомогательная таблица для расчета коэффициентов взаимной сопряженности из трех групп имеет следующий вид:
Коэффициенты взаимной сопряженности Пирсона и Чупрова изменяются от 0 до 1, но уже при значении 0,3 можно говорить о тесной связи между вариацией изучаемых признаков. В анализе социально - экономических явлений часто приходится прибегать к различным условным оценкам, например рангам, а взаимосвязь между признаками измерять с помощью непараметрических коэффициентов связи. Данные коэффициенты исчисляются при условии, что исследуемые признаки подчиняются различным законам распределения. Ранжирование - это процедура упорядочения объектов изучения, которая выполняется на основе предпочтения. Ранг - это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин. Если значения имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической от соответствующих номеров мест, которые определяют. Такие ранги называются связанными К непараметрическим ранговым коэффициентам связи можно отнести коэффициент корреляции знаков Фехнера, коэффициент корреляции рангов Спирмена, ранговый коэффициент корреляции Кендалла, Коэффициент корреляции знаков Фехнера основан на сопоставлении знаков отклонений от средней и подсчете числа случаев совпадения и несовпадения знаков, а не на сопоставлении попарно размеров отклонений индивидуальных значений факторного и результативного признаков от средней. Формула коэффициента корреляции знаков Фехнера
где а число пар с одинаковыми знаками отклонений х и у от Коэффициент Фехнера колеблется в пределах от -1 до +1. Чем ближе коэффициент к 1, тем теснее связь. Если Коэффициент корреляции рангов Спирмена исчисляется не по первичным данным, а по рангам (порядковым номерам),которые присваиваются всем значениям изучаемых признаков, расположенным в порядке предпочтительности. Если значения признаков совпадают, то определяется средний ранг. Коэффициент корреляции рангов Спирмена определяется по формуле:
где число рангов; Коэффициент корреляции рангов также колеблется от -1 до + 1. Если ранги по обеим признакам совпадают, то Коэффициент корреляции рангов Кендалла может также использоваться для измерения взаимосвязи между качественными и количественными признаками, ранжированными по одному принципу. Расчет рангового коэффициента Кендалла осуществляется по формуле;
где n-число наблюдений; S-сумма, включающая два слагаемых Р и Q, т.е. S=P+Q. Для нахождения Р нужно установить, сколько чисел, находящихся после каждого из элементов последовательности рангов переменной у, имеют величину ранга, превышающую ранг рассматриваемого элемента. Суммируя эти числа получают значение Р, которое можно рассматривать как меру соответствия последовательности рангов переменной у последовательности переменной х. Второе слагаемое Q характеризует степень несоответствия последовательности рангов переменной у последовательности рангов переменной х. Чтобы подсчитать Q определяют сколько чисел после каждого из членов последовательности рангов переменной у имеет ранг меньше, чем у рассматриваемого. Такие величины берутся со знаком минус. Коэффициент корреляции рангов Кендалла основан на сравнении общего итога суммы положительных и отрицательных баллов (S=P=Q) с максимальным значением одного из слагаемых. Коэффициент Кендалла также изменяется от -1 до +1 и равен кулю при отсутствия связи.
|

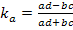 (1.7.29.)
(1.7.29.) (1.7.30.)
(1.7.30.)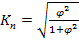 , где
, где  ,а
,а  или
или и Чупрова.
и Чупрова. (1.7.31.)
(1.7.31.) — число возможных значений первой статистической величины (число групп по столбцам);
— число возможных значений первой статистической величины (число групп по столбцам);  - число возможных значений второй статистической величины (число групп по строкам);
- число возможных значений второй статистической величины (число групп по строкам);  - показатель взаимной сопряженности (определяется как сумма отношений квадратов частот клетки таблицы распределения к произведению итоговых частот соответствующего столбца и строки).
- показатель взаимной сопряженности (определяется как сумма отношений квадратов частот клетки таблицы распределения к произведению итоговых частот соответствующего столбца и строки). .
. (1.7.32.)
(1.7.32.) и
и  ;
;  -число пар с разными знаками отклонений х и у от
-число пар с разными знаками отклонений х и у от >0 связь прямая, если
>0 связь прямая, если  (1.7.33.)
(1.7.33.)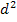 - квадрат разности рангов для каждой единицы, d = Rx — Ry; n-
- квадрат разности рангов для каждой единицы, d = Rx — Ry; n- 0, значит р=1 и связь полная прямая. Бели р=-1, то связь полная обратная. При р=0 связь отсутствует.
0, значит р=1 и связь полная прямая. Бели р=-1, то связь полная обратная. При р=0 связь отсутствует. (1.7.34.)
(1.7.34.)


