Статистическое моделирование связи методом корреляционного и регрессионного анализа
В общем виде задача статистики в области изучения взаимосвязей состоит не только в количественной оценке их наличия, направления и силы связи, но и в определении формы (аналитического выражения) влияния факторных признаков на результативный. Для ее решения применяют методы корреляционного и регрессионного анализа Задачи корреляционного анализа сводятся к измерению тесноты известной связи между варьирующими признаками, определению неизвестных причинных связей (причинный характер которых, должен быть выяснен с помощью теоретического анализа) и оценке факторов, оказывающих наибольшее влияние на результативный признак. Задачами регрессионного анализа являются выбор типа модели (формы связи), установление степени влияния независимых переменны на зависимую и определение расчетных значений, зависимой переменной (функции регрессии). Решение всех названных задач приводит к необходимости комплексного использования этих методов. Исследование связей в условиях массового наблюдения и действия случайных факторов осуществляется, как правило, с помощью экономико-статистических моделей. В широком смысле модель — это аналог, условный образ (изображение, описание, схема, чертеж и т.п.) какого-либо объекта, процесса или события, приближенно воссоздающий "оригинал". Модель представляет собой логическое или математическое описание компонентов и функций, отображающих существенные свойства моделируемого объекта или процесса, дает возможность установить основные закономерности изменения оригинала. В модели оперируют показателями, исчисленными для качественно однородных массовых явлений (совокупностей). Выражение модели в виде функциональных уравнений используют для расчета средних значений моделируемого показателя по набору заданных величин и для выявления степени влияния на него отдельных факторов. По количеству включаемых факторов модели могут быть однофакторными и многофакторными (два и более факторов). В зависимости от познавательной цели статистические модели подразделяются на структурные, динамические и модели связи. Рассмотрим основные проблемы статистического моделирования связи методами корреляционного и регрессионного анализа. Двухмерная линейная модель корреляционного и регрессионного анализа (однофакторный линейный корреляционный и регрессионный анализ). Наиболее разработанной в теории статистики является методология так называемой парной корреляции, рассматривающая влияние вариации факторного признака* на результативный признаку и представляющая собой однофакторный корреляционный и регрессионный анализ. Овладение теорией и практикой построения и анализа двухмерной модели корреляционного и регрессионного анализа представляет собой исходную основу для изучения многофакторных стохастических связей. Важнейшим этапом построения регрессионной модели (уравнения регрессии) является установление в анализе исходной информации математической функции. Сложность заключается в том, что из множества функций необходимо найти такую, которая лучше других выражает реально существующие связи между анализируемыми признаками. Выбор типа функции может опираться на теоретические знания об изучаемом явлении, опыт предыдущих аналогичных исследований, или осуществляться эмпирически — перебором и оценкой функций разных типов и т.п. При изучении связи экономических показателей производства (деятельности) используют различного вида уравнения прямолинейной и криволинейной связи. Внимание к линейным связям объясняется ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связи для выполнения расчетов преобразуют (путем логарифмирования или замены переменных) в линейную форму. Уравнение однофакторной (парной) регрессии имеет вид:
где Поскольку a0 является средним значением у в точке х = 0, экономическая интерпретация часто затруднена или вообще невозможна. Коэффициент парной линейной регрессии а1 имеет смысл показателя силы связи между вариацией факторного признака x и вариацией результативного признака у. Уравнение (5.3) показывает среднее значение изменения результативного признака у при изменении факторного признака х на одну единицу его измерения, т.е. вариацию у. приходящуюся на единицу вариации х. Знак а1 указывает направление этого изменения. Параметры уравнения а0, a1 находят методом наименьших квадратов (метод решения систем уравнений, при котором в качестве решения принимается точка минимума суммы квадратов отклонений), т.е. в основу этого метода положено требование минимальности сумм квадратов отклонений эмпирических данных yi от выровненных
Для нахождения минимума данной функции приравняем к нулю ее частные производные и получим систему двух линейных уравнений, которая называется системой нормальных уравнений:
Решим эту систему в общем виде:
Определив значения
Проверка адекватности регрессионной модели. Для практического использования моделей регрессии большое значение имеет их адекватность, т.е. соответствие фактическим статистическим данным. Корреляционный и регрессионный анализ обычно (особенно в условиях так называемого малого и среднего бизнеса) проводится для ограниченной по объему совокупности. Поэтому показатели регрессии и корреляции — параметры уравнения регрессии, коэффициенты корреляции и детерминации могут быть искажены действием случайных факторов. Чтобы проверить насколько зги показатели характерны для всей генеральной совокупности, не являются ли они результатом стечения случайных обстоятельств, необходимо проверить адекватность построенных статистических моделей. При численности объектов анализа до 30 единиц возникает необходимость проверки значимости (существенности) каждого коэффициента регрессии. При этом выясняют насколько вычисленные параметры характерны для отображения комплекса условий: не являются ли полученные значения параметров результатами действия случайных причин. Значимость коэффициентов простой линейной регрессии (применительно к совокупностям, у которых n < 30) осуществляют с помощью t-критерия Стьюдента. При этом вычисляют расчетные (фактические) значения t-критерия для параметра a0
для параметра a1
где n- объем выборки
(5.10) – среднее квадратическое отклонение результативного признака у от выравненных значений
Или
-среднеквадратическое отклонение факторного признака х от общей средней Вычисленные значения, сравнивают с критическими t, которые определяют по таблице Стьюдента с учетом принятого уровня значимости а и числом степеней свободы вариации v=n-2. В социально-экономических исследованиях уровень значимости а обычно принимают равным 0,05. Параметр признается значимым (существенным) при условии, если tрасч.>tтабл. В таком случае практически невероятно, что найденные значения параметров обусловлены только случайными совпадениями. Проверка адекватности регрессионной модели может быть дополнена корреляционным анализом. Для этого необходимо определить тесноту корреляционной связи между переменными х и у. Теснота корреляционной связи, как и любой другой, может быть измерена эмпирическим корреляционным отношением
где
Говоря о корреляционном отношении как о показателе измерения тесноты зависимости, следует отлипать от эмпирического корреляционного отношения — теоретическое. Теоретическое корреляционное отношение η представляет собой относительную величину, получающуюся в результате сравнения среднего квадратического отклонения выровненных значений результативного признака
где
Тогда результативного признака.
Изменение значения η объясняется влиянием факторного признака. В основе расчета корреляционного отношения лежит правило сложения дисперсий, т.е.
где
Тогда формула теоретического корреляционного отношения примет вид:
или Подкоренное выражение корреляционного отношения представляет собой коэффициент детерминации (меры определенности, причинности). Коэффициент детерминации показывает долю вариации результативного признака под влиянием вариации признака-фактора. Теоретическое корреляционное отношение применяется для измерения тесноты связи при линейной и криволинейной зависимостях между результативным и факторным признаком. При криволинейных связях теоретическое корреляционное отношение, исчисляемое по вышеприведенным формулам часто называют индексом корреляции R. Как видно из приведенных формул, корреляционное отношение может находиться в пределах от 0 до 1, т.е. (0<η<1). Чем ближе корреляционное отношение к 1, тем связь между признаками теснее. Кроме того, при линейной форме уравнения применяется другой показатель тесноты связи — линейный коэффициент корреляции:
Или Для практических вычислений при малом числе наблюдений n≤20÷30 линейный коэффициент корреляции исчисляют по формуле:
Значение линейного коэффициента корреляции важно для исследования социально-экономических явлений и процессов, распределение которых близко к нормальному. Он принимает значения в интервале: -1 < г < 1. Отрицательные значения указывают на обратную связь, Квадрат линейного коэффициента корреляции г2 называется линейным коэффициентом детерминации. Из определения коэффициента детерминации очевидно, что его числовое значение всегда заключено и пределах от 0 до 1, т.е. 0 ≤ г2 ≤1. Степень тесноты связи полностью соответствует теоретическому корреляционному отношению, которое является более универсальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции. Факт совпадений и несовпадений значений теоретического корреляционного отношения η и линейного коэффициента корреляции г используется для оценки формы связи. Выше отмечалось, что посредством теоретического корреляционного отношения измеряется теснота связи любой формы, а с помощью линейного коэффициента корреляции — только прямолинейной. Следовательно, значения η и г2 совпадают только при наличии прямолинейной связи. Несовпадение этих величин свидетельствует, что связь между изучаемыми признаками не прямолинейная, а криволинейная. Установлено, что если разность квадратов η2 и г2 не превышает 0,1, то гипотезу о прямолинейной форме связи можно считать подтвержденной. Показатели тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, могут искажаться действием случайных причин. Это вызывает необходимость проверки их существенности, дающей возможность распространять выводы по результатам выборки на генеральную совокупность. Для оценки значимости коэффициента корреляции г используют t-критерий Стьюдента, который применяется при t- распределении, отличном от нормального. При линейной однофакторной связи t-критерий можно рассчитать по формуле:
где (n-2) — число степеней свободы при заданном уровне значимости α, и объеме выборки n. Полученное значение Экономическая интерпретация параметров регрессии. После проверки адекватности, установления точности и надежности построенной модели (уравнения регрессии) ее необходимо проанализировать. Прежде всего нужно проверить согласуются ли знаки параметров с теоретическими представлениями и соображениями о направлении влияния признака -фактора на результативный признак (показатель). Для удобства интерпретации параметра а1 используют коэффициент эластичности. Он показывает средние изменения результативного признака при изменении факторного признака на 1 % и вычисляется по формуле, %:
|

 (1.7.3.)
(1.7.3.) -теоретические значения результативного признака, полученные по уравнению регрессии; а0, a1 — коэффициенты (параметры) уравнения регрессии.
-теоретические значения результативного признака, полученные по уравнению регрессии; а0, a1 — коэффициенты (параметры) уравнения регрессии.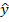 :
: (1.7.4.)
(1.7.4.) (1.7.5.)
(1.7.5.) (1.7.6.)
(1.7.6.) (1.7.7.)
(1.7.7.) и подставив их в уравнение связи
и подставив их в уравнение связи находим значения
находим значения 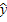 х , зависящие только от заданного значения х.
х , зависящие только от заданного значения х. (1.7.8.)
(1.7.8.) (1.7.9.)
(1.7.9.) (1.7.10.)
(1.7.10.)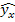
 (1.7.11.)
(1.7.11.) (1.7.12.)
(1.7.12.) .
.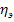 , когда
, когда 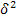 (межгрупповая дисперсия) характеризует отклонения групповых средних результативного признака от общей средней:
(межгрупповая дисперсия) характеризует отклонения групповых средних результативного признака от общей средней: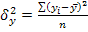 (1.7.13.)
(1.7.13.) - общая дисперсия результативного признака.
- общая дисперсия результативного признака. (1.7.14.)
(1.7.14.) (1.7.15.)
(1.7.15.) т.е. рассчитанных по уравнению регрессии, со средним квадратаческим отношением эмпирических (фактических) значений результативности признака
т.е. рассчитанных по уравнению регрессии, со средним квадратаческим отношением эмпирических (фактических) значений результативности признака  :
: (1.7.16.)
(1.7.16.) - дисперсия выровненных значений результативного признака
- дисперсия выровненных значений результативного признака (1.7.18.)
(1.7.18.) (1.7.19.)
(1.7.19.)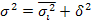 (1.7.20.)
(1.7.20.) - отражает вариацию у за счет всех остальных факторов, кроме X, т.е. является остаточной дисперсией:
- отражает вариацию у за счет всех остальных факторов, кроме X, т.е. является остаточной дисперсией: (1.7.21.)
(1.7.21.)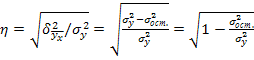 (1.7.22)
(1.7.22)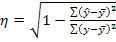 (1.7.23.)
(1.7.23.) (1.7.24.)
(1.7.24.)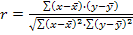 (1.7.25.)
(1.7.25.) (1.7.26.)
(1.7.26.) (1.7.27.)
(1.7.27.)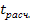 сравнивают с табличным значением t-критерия (для α = 0,05 и 0,01). Если рассчитанное значение
сравнивают с табличным значением t-критерия (для α = 0,05 и 0,01). Если рассчитанное значение  то практически невероятно, что найденное значение обусловлено только случайными колебаниями (т.е. отклоняется гипотеза о его случайности).
то практически невероятно, что найденное значение обусловлено только случайными колебаниями (т.е. отклоняется гипотеза о его случайности). (1.7.28.)
(1.7.28.)


