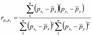 В практических задачах все чаще требуется измерение связей неколичественных переменных, измеренных на номинальных и порядковых шкалах. Исп. Рейтинг – по сути порядковая переменная, и для изучения зависимости рейтинга от каких-либо характеристик должны использоваться меры связи, предназначенные для порядковых переменных. При этом единицам совокупности присваиваются ранги по разным признакам, т.е. порядковые номера единиц совокупности в ранжированном ряду. Связь между ними определяется коэффициентом корреляции рангов. Коэффициент корреляции рангов Спирмена:
В практических задачах все чаще требуется измерение связей неколичественных переменных, измеренных на номинальных и порядковых шкалах. Исп. Рейтинг – по сути порядковая переменная, и для изучения зависимости рейтинга от каких-либо характеристик должны использоваться меры связи, предназначенные для порядковых переменных. При этом единицам совокупности присваиваются ранги по разным признакам, т.е. порядковые номера единиц совокупности в ранжированном ряду. Связь между ними определяется коэффициентом корреляции рангов. Коэффициент корреляции рангов Спирмена:
где pxi и pyi - ранги i -ой единицы совок. по перем. x и y; px(сред) и py(cред) - сред. ранги по пер. x и y.
 Путем преобразования приведенной формулы Спирмен получил выражение коэффициента ранговой корреляции:
Путем преобразования приведенной формулы Спирмен получил выражение коэффициента ранговой корреляции:
di - разность рангов по переменным x и y для i- ой ед. совок. Значимость коэффициента корреляции рангов можно проверить по t-критерию Стьюдента:

 По таблице распределения Стьюдента находится критическое значение t – критерия. Если t>t таблич, то rpxpy значим. При определении t табл. используется число степеней свободы (df=n-2): Уровень значимости а=1 – доверительная вероятность. Значимость коэф. корреляц. рангов можно проверить по таблице предельных значений коэффициентов корреляции рангов Спирмена. Коэффициент корреляции рангов Кендэла дает более строгую оценку связей: S – фактическая сумма рангов, знаменатель - макс сумма рангов.
По таблице распределения Стьюдента находится критическое значение t – критерия. Если t>t таблич, то rpxpy значим. При определении t табл. используется число степеней свободы (df=n-2): Уровень значимости а=1 – доверительная вероятность. Значимость коэф. корреляц. рангов можно проверить по таблице предельных значений коэффициентов корреляции рангов Спирмена. Коэффициент корреляции рангов Кендэла дает более строгую оценку связей: S – фактическая сумма рангов, знаменатель - макс сумма рангов.
S рассчитывается по рангам у. Для каждого ранга определяется число последующих рангов выше данного и вычитается число последующих рангов ниже данного. Измерение тесноты связи между номинальными переменными на основе таблиц сопряженности. (таблицы, в которых дается распределение по двум или более признакам.)

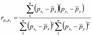 В практических задачах все чаще требуется измерение связей неколичественных переменных, измеренных на номинальных и порядковых шкалах. Исп. Рейтинг – по сути порядковая переменная, и для изучения зависимости рейтинга от каких-либо характеристик должны использоваться меры связи, предназначенные для порядковых переменных. При этом единицам совокупности присваиваются ранги по разным признакам, т.е. порядковые номера единиц совокупности в ранжированном ряду. Связь между ними определяется коэффициентом корреляции рангов. Коэффициент корреляции рангов Спирмена:
В практических задачах все чаще требуется измерение связей неколичественных переменных, измеренных на номинальных и порядковых шкалах. Исп. Рейтинг – по сути порядковая переменная, и для изучения зависимости рейтинга от каких-либо характеристик должны использоваться меры связи, предназначенные для порядковых переменных. При этом единицам совокупности присваиваются ранги по разным признакам, т.е. порядковые номера единиц совокупности в ранжированном ряду. Связь между ними определяется коэффициентом корреляции рангов. Коэффициент корреляции рангов Спирмена: Путем преобразования приведенной формулы Спирмен получил выражение коэффициента ранговой корреляции:
Путем преобразования приведенной формулы Спирмен получил выражение коэффициента ранговой корреляции:
 По таблице распределения Стьюдента находится критическое значение t – критерия. Если t>t таблич, то rpxpy значим. При определении t табл. используется число степеней свободы (df=n-2): Уровень значимости а=1 – доверительная вероятность. Значимость коэф. корреляц. рангов можно проверить по таблице предельных значений коэффициентов корреляции рангов Спирмена. Коэффициент корреляции рангов Кендэла дает более строгую оценку связей: S – фактическая сумма рангов, знаменатель - макс сумма рангов.
По таблице распределения Стьюдента находится критическое значение t – критерия. Если t>t таблич, то rpxpy значим. При определении t табл. используется число степеней свободы (df=n-2): Уровень значимости а=1 – доверительная вероятность. Значимость коэф. корреляц. рангов можно проверить по таблице предельных значений коэффициентов корреляции рангов Спирмена. Коэффициент корреляции рангов Кендэла дает более строгую оценку связей: S – фактическая сумма рангов, знаменатель - макс сумма рангов.


