Критерий Пирсона (сравнение эмпирического распределения с теоретическим).Критерий применяется в 2-х случаях: 1) для сопоставления эмпирического распределения признака теоритическому; 2) для сопоставления 2х или более эмпирических распределений одного и того же признака. Критерий построен так, что при полном совпадении экспериментального и теоритического (или 2х экспериментальных) распределений величина Основная расчётная формула критерия f - частота Расчётная формула для сравнения 2-х эмпирических распределений выглядит так:
Если при расчёте критерия данные даются в виде таблицы, то число степеней свободы находится по формуле:
Рассмотрим на примере сравнение эмпирического распределения с теоритическим. Пусть эксперимент состоит в том, чтобы убедиться, является ли конкретный игральный шестигранный кубик с цифрами на гранях от 1 до 6 «идеальным». Подбросим кубик 60 раз и составим таблицу полученных данных.
15, 08 α = 0,01
Поскольку эмп. значение критерия Рассмотрим теперь пример использования измерений в дихотомической шкале. Испытуемым предлагалось выбрать левый или правый стол с заданиями. Было сообщено, что задания на обоих столах одинаковые. Из 150 участников эксперимента правый стол выбрали 98 человек, левый - 52. Можно ли утверждать, что существует какая-то причина предпочтения выбора?
Сумма должна быть равна 0, если не равна 0, то нужно искать вычислительную ошибку.
6,64 α = 0, 01
Поскольку
|
= 0 и чем больше расхождение между распределениями, тем больше величина 
выглядит так: 
∙ 
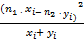
и 
- числа элементов, составляющих первую и вторую выборки. Они могут совпадать, а могут и не совпадать.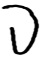
= (k - 1) (c - 1); k - кол-во строк, c - столбцов.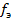
+ 
+ 
+ 
+ 
+ 
= 
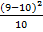= 4,2
= 11,07 α = 0,05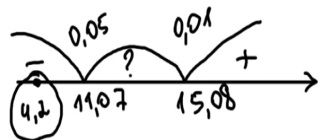
об отсутствии различий и поэтому делаем вывод о том, что наш кубик «безупречен».
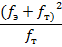
= 2-1 = 1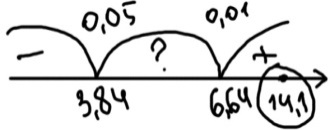
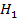о существовании различий. Следовательно можно утверждать, что существует какая-то причина предпочтения выбора.
