Критерий Пирсона (сравнение двух эмпирических распределений)
Критерий применяется в 2-х случаях: 1) для сопоставления эмпирического распределения признака теоритическому; 2) для сопоставления 2х или более эмпирических распределений одного и того же признака. Критерий построен так, что при полном совпадении экспериментального и теоритического (или 2х экспериментальных) распределений величина Основная расчётная формула критерия f - частота Расчётная формула для сравнения 2-х эмпирических распределений выглядит так:
Если при расчёте критерия данные даются в виде таблицы, то число степеней свободы находится по формуле: На практике значительно чаще встречаются задачи, в которых необходимо сравнивать не экспериментальное с теоритическим, а 2 экспериментальных распределения. Рассмотрим следующий пример. Одинаков ли уровень подготовленности учащихся в 2-х школах, если в 1-й школе из 100 человек поступили в ВУЗ 82 человека, а во 2-й из 87 - 44? Представим данные задачи в виде четырёхпольной таблицы, ячейки которой будет обозначать буквами A, B, C, D.
Теоритические частоты в подобных случаях вычисляются на основе эмпирических разными способами в зависимости от типа решаемой задачи. Важно сразу определить, что будем считать долей признака. Из таблицы видно, что 18 и 43 чел-ка соответственно из1й и 2й школ не поступили в ВУЗ. Относительно этих величин подсчитаем так называемую долю признака непоступаимости. P = Теперь подсчиатем сколько учащихся из каждой школы теоритически не должны были поступить в ВУЗ. Теперь понятно, как подсчитать число теоритически поступивших.
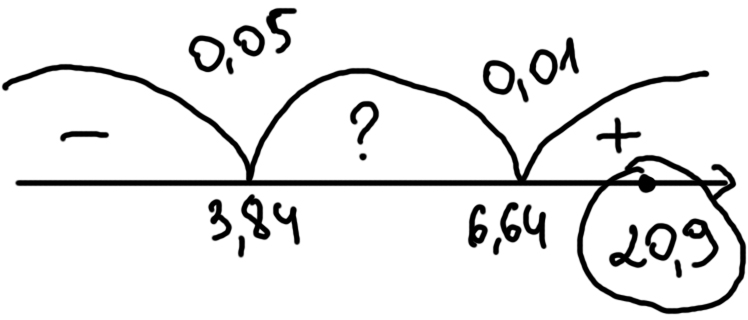
6, 64 α = 0,01
Таким образом, нужно применить гипотезу о наличии различий между двумя эмпирическими распределениями. Т.о. ур-нь подготовки в 2-х школах оказался различным. Преимущества критерия
|

 = 0 и чем больше расхождение между распределениями, тем больше величина
= 0 и чем больше расхождение между распределениями, тем больше величина  выглядит так:
выглядит так: 
 ∙
∙ 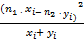
 и
и  - числа элементов, составляющих первую и вторую выборки. Они могут совпадать, а могут и не совпадать.
- числа элементов, составляющих первую и вторую выборки. Они могут совпадать, а могут и не совпадать.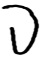 = (k - 1) (c - 1); k - кол-во строк, c - столбцов
= (k - 1) (c - 1); k - кол-во строк, c - столбцов =(примерно) 0,33
=(примерно) 0,33 = 0,33 · 100 = 33;
= 0,33 · 100 = 33;  = 0,33 ∙ 87 = 8,71
= 0,33 ∙ 87 = 8,71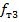 = 100 - 33 = 67;
= 100 - 33 = 67;  = 87 - 28,71 = 58, 29
= 87 - 28,71 = 58, 29 +
+  +
+ 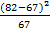 +
+ 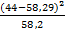 = 20,9
= 20,9 = (2 - 1) (2 - 1) = 1
= (2 - 1) (2 - 1) = 1 = 3, 84 α = 0,05
= 3, 84 α = 0,05