Коэффициент ранговой корреляции Кендала
Коэф ранг-й корел Кендала обозначается Алгоритм применения коэ-та (тау) 1)Данные экспер-та ранжируются для каждой переменной отдельно 2)Составляется таблица которая содержит столбцы: -«первая переменная» (напр xi); -«2-я перем-я» (напр yi); - «совпадения»; -«инверсии» 3)Ранги переменных заносятся в таблицу таким образом, чтобы один из ранговых рядов (как правило 1-й) располагается в порядке возрастания. 4)Для каждого значения ранга второй переменной подсчитывается кол-вонижестоящих рангов, которые больше чем рассматриваемое значение и это кол-во заносят в столбец совпадения; 5)Для каждого значения ранга второй переменной подсчитывают кол-во нижестоящих значений рангов, которые меньше чем рассматриваемые значения и это кол-во заносят в столбец инверсии. 6)Число совпадений обознач через P, число инверсий через Q; для проверки правильности совершённых действий используется формула P+Q = 7)Для нахождения значения коэф-та (значок тау) используется 3 формулы, которые дают одно и тоже знач-е и отличаются только удобством 1. 2. Ɩ ̃= 1 - 3. 8)По табл находим кр знач-я коэф-та тау для уровней значимости p=0,05 и 0,01. 9)Если таблицы кр знач коэф-та тау отсутствуют, то как и в случае коэф-та коррел Пирсона можно воспользоваться таблицами кр знач-й Стюдента, вычислив коэф-т Стьюдента по формуле t = Число степ свободы определяется так: K=n-2
|

 (тау). Коэф-т предначначен для работы с переменными полученными в ранговой шкале, этот коэф-т может быть использован всместо коэф-та ранговой корреляции Спирмена, поскольку явл более простым по способу расчёта, он основан на подсчёте суммы совпадений и инверсии. Применение этого коэф-та возможно только в случае отсутствия одинаковых рангов.
(тау). Коэф-т предначначен для работы с переменными полученными в ранговой шкале, этот коэф-т может быть использован всместо коэф-та ранговой корреляции Спирмена, поскольку явл более простым по способу расчёта, он основан на подсчёте суммы совпадений и инверсии. Применение этого коэф-та возможно только в случае отсутствия одинаковых рангов.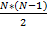 , кроме того следует помнить, что сумма числа совпадений и числа инверсий с каждой новой строкой уменьшается на 1.
, кроме того следует помнить, что сумма числа совпадений и числа инверсий с каждой новой строкой уменьшается на 1.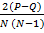

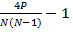
 *
* 



