Корреляционно-регрессионный анализ.
Изучение корреляционных связей сводится в основном к решению следующих задач: • выявление наличия (или отсутствия) корреляционной связи между изучаемыми признаками. Эта задача может быть решена на основе параллельного сопоставления (сравнения) значений х и у у п единиц совокупности; • измерение тесноты связи между двумя (и более) признаками с помощью специальных коэффициентов. Эта часть исследования именуется корреляционным анализом; • определение уравнения регрессии — математической модели, в которой среднее значение результативного признака у рассматривается как функция одной или нескольких переменных — факторных признаков. Эта часть исследования именуется регрессионным анализом. Последовательность рассмотрения перечисленных задач, естественно, может меняться в каждом конкретном исследовании. Общий термин «корреляционно-регрессионный анализ» подразумевает всестороннее исследование корреляционных связей, в том числе нахождение уравнений регрессии, измерение тесноты и направления связи, а также определение возможных ошибок, как параметров уравнений регрессии, так и показателей тесноты связи. Измерить корреляционную связь между признаками х и у и найти форму этой связи, ее аналитическое выражение (математическую модель) — две важные, неразрывные и дополняющие друг друга задачи корреляционно-регрессионного анализа. Найти уравнение регрессии — значит по эмпирическим (фактическим) данным математически описать изменения взаимно коррелируемых величин. Уравнение регрессии должно определить, каким будет среднее значение результативного признака у при том или ином значении факторного признака х, если остальные факторы, влияющие на у и не связанные с х, не учитывать, т.е. абстрагироваться от них. Другими словами, уравнение регрессии можно рассматривать как связь средней величины результативного признака у со значениями факторного признака х. Уравнение регрессии можно также назвать теоретической линией регрессии. Рассчитанные по уравнению регрессии значения результативного признака называются теоретическими, обычно обозначаются Найти в каждом конкретном случае тип функции, с помощью которой можно наиболее адекватно отразить ту или иную зависимость между признаками х и у, — одна из основных задач регрессионного анализа. Выбор теоретической линии регрессии часто обусловлен формой эмпирической линии регрессии; теоретическая линия как бы сглаживает изломы эмпирической линии регрессии. Кроме того, необходимо учитывать природу изучаемых показателей и специфику их взаимосвязей. Для аналитической связи между х и у могут использоваться следующие простые виды уравнений: а) yх = a0+a1 x (прямая); б) ух = а0 + а1 х + а2x2 (парабола 2-го порядка); в) ух= a0 + a1 * 1/x (гипербола); г) ух = а0а1x (показательная функция); д) yx=a + a1 lgx (логарифмическая функция) и др. Обычно зависимость, выражаемую уравнением прямой, называют линейной (или прямолинейной),а все остальные — криволинейными. Выбрав тип функции, по эмпирическим данным определяют параметры уравнения. При этом отыскиваемые параметры должны быть такими, при которых рассчитанные по уравнению теоретические значения результативного признака ух были бы максимально близки к эмпирическим данным. Существует несколько методов нахождения параметров уравнения регрессии. Наиболее часто используется метод наименьших квадратов (МНК). Его суть заключается в следующем требовании: искомые теоретические значения результативного признака ух должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических значений, т.е. Если данное требование соблюдается, легко определить, при каких значениях а0, а1, и т.д. для каждой аналитической кривой эта сумма квадратов отклонений будет минимальной. Линейная зависимость — наиболее часто используемая форма связи между двумя коррелируемыми признаками, и выражается она при парной корреляции уравнением прямой: ух = а0 + а1х. Гипотеза именно о линейной зависимости между х и у выдвигается в том случае, если результативный и факторный признаки возрастают (или убывают) примерно одинаково. Параметры а0 и а1, отыскиваются по МНК следующим образом. Согласно требованию МНК при линейной зависимости в формуле вместо Дальнейшее решение сводится к задаче на экстремум, т.е. к определению того, при каком значении а0 и а1, функция двух переменных S может достигнуть минимума. Для этого надо найти частные производные S по а0 и а1, приравнять их к нулю и после элементарных преобразований решить систему двух уравнений с двумя неизвестными. Найдем частные производные:
Эта система называется системой нормальных уравнений МНК для линейного уравнения регрессии. Для решения системы по эмпирическим (наблюдаемым) данным определяется число единиц наблюдения п, и входящие в систему суммы. Подставив вычисленные суммы в систему нормальных уравнений, находятся параметры искомой прямой (линейного уравнения регрессии). Пример. Рассчитать параметры уравнения регрессии между экспортом х и валовым внутренним продуктом у за последние девять лет по следующим данным: Таблица 5. Расчетная таблица для нахождения параметров уравнения регрессии.
Параметры уравнения регрессии найдем, решив систему нормальных равнений, предварительно подставив в нее необходимые суммы, рассчитанные в таблице:
Решением данной системы будет: а0 = 309,85, а1 =2,628. Отсюда искомое уравнение регрессии: Подставляя в данное уравнение последовательно значения х, находим теоретические (выравненные) значения результативного признака у, которые показывают, каким теоретически должен быть объем валового выпуска продукции при данной стоимости основных фондов хi (при прочих равных условиях для всех предприятий). Параметр а1 в уравнении линейной регрессии называется коэффициентом регрессии, который показывает, на сколько (в абсолютном выражении) изменяется значение результативного признака у при изменении факторного признака х на единицу.
|

 (читается: «игрек, выравненный по х») и рассматриваются как функция от х, т.е. ух = f(x).
(читается: «игрек, выравненный по х») и рассматриваются как функция от х, т.е. ух = f(x). (минимизируются квадраты отклонений, поскольку
(минимизируются квадраты отклонений, поскольку  ).
).

 Сократив каждое уравнение на (-2), раскрыв скобки и перенеся члены с х в одну сторону, а с у — в другую, получим:
Сократив каждое уравнение на (-2), раскрыв скобки и перенеся члены с х в одну сторону, а с у — в другую, получим: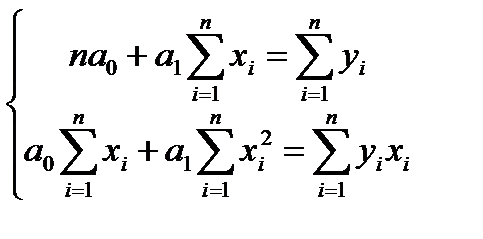


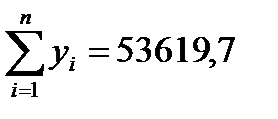




 .
.


