Задача 22. Продажа масла в магазине по кварталамПродажа масла в магазине по кварталам. Вычислить цепные и базисные, индивидуальные и общие индексы физического объема и цен. Реализация масла в магазинах за три квартала
1. Индивидуальные индексы (на примере масла в пачках): а) физического объема цепные: базисные: Взаимосвязь индексов: Произведение цепных индексов равно базисному за тот же период времени: Частное от деления двух базисных индексов равно цепному за тог же период времени: б) цен цепные: базисные: 2. Общие индексы физического объема (по методике Ласпейреса): цепные: базисные: Взаимосвязь индексов: 1) цепных: 2) базисных: 3. Общие индексы цен (по методике Пааше): цепные: базисные:
Взаимосвязь: то есть произведение цепных индексов не равно базисному из-за переменных весов.
Задача 23. (корреляционно-регрессионный анализ) Имеются данные исследования влияния электровооруженности труда на выработку рабочих на пяти предприятиях отрасли. Определить взаимосвязь между выработкой рабочих и электровооруженностью труда и проверить ее значимость. Аналитическое выражение связи проверить на достоверность при уровне значимости α = 0,05.
Показатели работы предприятий отрасли
Сравнение параллельных рядов таблицы показывает также наличие связи: с ростом электровооруженности растет выработка, направление - прямая связь. Вычисляем линейный коэффициент корреляции, для чего составляем вспомогательную таблицу1:. Таблица 1. -Вычисление линейного коэффициента корреляции
Он принимает значения в интервале -1 < г ≤ 1. Если значение отрицательное, то между показателями существует обратная связь; если положительное - прямая. Если r = 0, линейная связь отсутствует, т.е. величины х и у независимы, от 0,1 до 0,3 - слабая; 0,3 - 0,7 - средняя, 0,7 – 0,999 - тесная. Если r = 1, то связь между признаками х и у функциональная, т.е. каждому значению факторного признака строго соответствует одно значение результативного признака. Значение r = 0,98 означает, что между электровооруженностью рабочих и производительностью труда существует прямая тесная связь, т.е. с увеличением х увеличивается у. Значимость линейного коэффициента корреляции проверяется по t -критерию Стьюдента по формуле Если при уровне значимости α = 0,05 эмпирическое значение tрасч >tтабл,то линейный коэффициент корреляции является значимым.
Табличное значение t - критерия при α - 0,05 и числе степеней свободы v = п - 2 = 5 - 2 = 3 равно 2,571; tpacч > tтабл,и коэффициент корреляции можно признать значимым. Далее найдем Уравнение связи Уравнение однофакторной (парной) линейной корреляционной связи имеет вид: где п - число единиц изучаемой совокупности; х - признак-фактор, положенный в основу группировки; у - результативный признак.В соответствии с изучаемыми показателями, система нормальных уравнений имеет вид: Решаем систему уравнений методом Гаусса: каждое уравнение делим на коэффициент при a0: _ 9,28 а1= 5,71 8,76 а1= 5,20, а1 = 0,51:0,52 = 0,981. 0,52 а1= 0,51 Затем подставляем значение а1 в первое уравнение и находим а0: а0 + 8,76 а1 = 5,2; а0 + 8,594 = 5,2; а0 = 5,2 - 8,594 = - 3,394. Параметр а0 - свободный член уравнения можно приближенно интерпретировать как количественную характеристику влияния всех факторов, кроме изучаемого х. Параметр а1 показывает, в какой мере увеличивается (или уменьшается) значение результативного признака у с изменением (ростом) фактора х на единицу. С ростом электровооруженности на 1 чел. на 1 кВт/ч производительность труда (выработка) растет на 981 р. Модель уравнения имеет вид: Подставляя значение х в уравнение, находим Имеется явная тенденция роста выработки с увеличением злектровооруженности рабочих. Для практического использования моделей регрессии производят их проверку на адекватность, т.е. соответствие фактическим данным. Оценка адекватности регрессионной модели производится по формуле с помощью критерия Фишера: При численности изучаемой совокупности п<;30 единиц необходимо проверять значимость (существенность) каждого коэффициента регрессии. При этом выясняют, насколько вычисленные параметры характерны для отображения комплекса условий: не являются ли полученные значения параметров результатом действия случайных причин. Значимость коэффициентов проверяется с помощью t - критерия Стьюдента. Вычисляют расчетные (фактические) значения t - критерия:
где п - объем изучаемой совокупности;
Таблица 2. - Расчетные значения для вычисления дисперсии
Остаточная дисперсия: Факторная дисперсия: Эмпирическое значение критерия Фишера: Табличное значение FT при α = 0,05 и числе степеней свободы (2 - 1), (5 - 2) равно 10,18. Следовательно, FЭ > FT, и уравнение связи можно признать адекватным. Оценим значимость параметров уравнения регрессии; Расчетные значения t - критерия:
По таблице распределения Стьюдента для числа степеней свободы v = п - 2 = 5-2 = 3находим критическое значение t - критерия (при α= 0,05, v = 3): tma6л = 3,182. Следовательно, tpaсч > tтабл, и оба параметра а0 и а1 являются значимыми, а не результатом стечения случайных обстоятельств. Вычислим теоретическое корреляционное отношение ηпо расчетам вычислений табл. 1 и 2: Из предыдущих вычислений
Это значит, что 96% от общей вариации производительности труда в изучаемой бригаде обусловлено вариацией электровооруженности рабочих, и только (100 - 96) = 4% нельзя объяснить изменением изучаемого фактора, т.е. оказывают влияние прочие, неучтенные факторы. Теоретический коэффициент корреляции Таким образом, построенная регрессионная модель зависимости выработки рабочих от электровооруженности Он характеризует количественную зависимость между признаками. Признаки могут рассматриваться по фактическим и теоретическим уровням. Коэффициент эластичности исчисляется в абсолютных и относительных величинах по формулам:
Определить абсолютную и относительную эластичность между 3 и 4 предприятиями по исходным данным. Сделать оценку эластичности.
Увеличение на 4 предприятии по сравнению с 3 электровооруженности на 1 чел. на 1 кВт/ч увеличило выработку на 1333 р.
Увеличение на 4 предприятии по сравнению с 3 электровооруженности на 1 % увеличило выработку на 2,27% Он показывает средние изменения результативного признака у при изменении факторного признака х на 1% и вычисляется по формуле (в %):
Для рассматриваемого примера из предыдущих вычислений Данный вывод справедлив только для изучаемой совокупности при конкретных условиях работы. Если данная совокупность и условия работы типичны, то коэффициент регрессии может быть использован для нормирования и планирования производительности труда рабочих. Спрогнозируем значение выработки, если электровооруженность будет равна 15,0 кВт/ч на одного рабочего. Подставляем значение х = 15,0 в уравнение регрессии:
При электровооруженности труда 15,0 кВт/ч на одного рабочего выработка должна составить 11321 р.
|
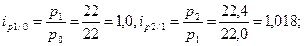
,где 
. Для нахождения минимума данной функции приравнивают частные производные к нулю и получают систему нормальных уравнений: 
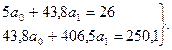
откуда
где т - число параметров модели; n - число единиц наблюдения. Эмпирическое значение критерия FЭ сравнивается с табличным (критическим) FТ при уровне значимости α - 0,05 и числом степеней свободы (m - 1), (n - m). Если FЭ > FT, уравнение регрессии признается значимым.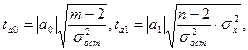
- остаточная дисперсия результативного признака у от выравненных значений 
. Расчетные (фактические) значения t - критерия сравниваются со значениями по таблице Стьюдента при уровне значимости α= 0,05 или α = 0,01 и числом степеней свободы (n - 2). Параметр является значимым, если эмпирическое значение t больше табличного, tpaсч > tтабл. Для оценки адекватности модели связи и значимости параметров строим вспомогательную таблицу 2:
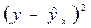
Вначале вычислим коэффициент детерминации: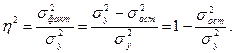 
что указывает на тесную связь между признаками х и у.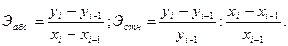
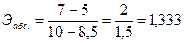тыс.р.
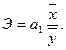
т.е. при увеличении электровооруженности рабочих на 1 % следует ожидать повышения производительности труда на 1,65%.
