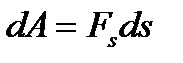Айналмалы қатты дененің динамикасының негізгі теңдеуі
Дене ∆φ бұрышқа бұрылғанда күш түсірілген А нүктесі ∆S доғасының ұзындығына жылжиды, сонда F күшінің істеген жұмысы: dA=FdS; мұндағы dS=rd φ; сонда dA=Frd φ болады. Егер M=Fr, болса dA=Md φ; бұдан дененің айналдыру жұмысы кинетикалық энергияны ұлғайтуға кетеді:
M=Jε немесе Бұл теңдеу айналмалы қатты дененің қозғалыс динамикасының негізгі теңдеуі болып табылады. Векторлық түрде
Қатты дене жеке бөлшегінің импульс моменті деп бөлшектің импульсінің айналу осіне дейінгі қашықтыққа көбейтіндісін айтады.
Қатты дененің импульс моменті оның жеке бөлшектерінің импульс моменттерінің қосындысына тең:
Яғни: L=Jω векторлық шама. Оның бағыты бұрыштық жылдамдық бағытымен сәйкес.
Онда импульс моменті өрнегі векторлық түрде Импульс моменті векторы импульс векторының радиус-векторға векторлық көбейтіндісіне тең.
немесе Бұл теңдеу айналмалы қозғалыс заңының тағы бір түрі: Импульс моментінің уақыт бойынша туындысы осы оське қарағандағы күш моментіне тең. Егер жүйе тұйық болса, яғни Бұл теңдеу импульс моментінің сақталу заңының өрнегі: Тұйық жүйенің импульс моменті сақталады, яғни уақыт бойынша өзгермейді. Импульс моментінің сақталу заңы табиғаттың фундаментальді заңдарының бірі. Ол кеңістіктің симметриялық қасиетімен оның изотроптығымен байланысы, яғни физикалық заңдардың санақ жүйесінің координат осьтерінің бағытына инварианттылығын көрсетеді. Дененің ілгерілмелі қозғалысы мен қатты дененің айналмалы қозғалысын салыстырайық;:
|

 яғни қорыта келгенде мына түрдегі теңдеу шығады:
яғни қорыта келгенде мына түрдегі теңдеу шығады: (3.8)
(3.8) :
:


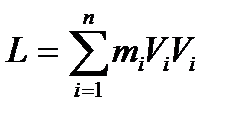
 өрнегін қойсақ:
өрнегін қойсақ: (3.9)
(3.9) . (3.10)
. (3.10) түрінде жазылады.
түрінде жазылады. (3.11)
(3.11) ,онда
,онда  екені түсінікті. (3.10) – дан
екені түсінікті. (3.10) – дан  (3.12)
(3.12)