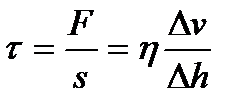Бернулли теңдеуі
Ағын түтігі ішінде қозғалған сұйықтың жылдамдығы мен қысымының арасындағы байланысты қарастырайық. Ол үшін
Бұл қималардағы толық энергияның өзгерісі сұйықтың орын ауыстыру жұмысына тең:
Мұндағы
Бұл теңдікті кез келген қима үшін жазып, Бернулли теңдеуін аламыз:
Мұндағы Бернулли теңдеуі – идеал сұйықтың ағысына арналған энергияның сақталу заңы болып табылады, яғни түтіктен аққан сұйықтың қысымы қозғалыс жылдамдығы аз жерде-көп, ал қозғалыс жылдамдығы көп жерде – аз. Бернулли теңдеуінің қолданылуына мысал: ыдыстағы сұйықтың тесіктен сорғалап ағуын қарастырайық: Екі қима үшін Бернулли теңдеуін жазайық:
Ал
Бұл теңдеу Торричелли теңдеуі деп аталады.
Тұтқырлық; Барлық нақты сұйықтардың бір қабаты екінші қабатымен салыстырғанда орын ауыстырса, онда үйкеліс күші пайда болады. Осы үйкеліс күшін тұтқырлық деп атайды. Сұйықтың бірінші қабатынан екіншісіне өткенде жылдамдығының өзгеруі, жылдамдық градиенті деп атайды. Ньютон,алғаш рет сұйықтың екі қабатының арасындағы үйкеліс күші, жылдамдықтар айырымы мен жанасып тұрған сұйық қабырғасы бетінің ауданына тура пропорционал және сол қабаттың ара қашықтығына кері пропорционал екендігін дәлелдейді:
Мұндағы Сұйық тұтқырлық әсерінен болатын қозғалыс кезіндегі жанама кернеулігі мынадай:
Тұтқырлықтың өлшем бірлігі – (Па*с) Тұтқырлықтың берілген сұйықтың тығыздығына қатынасы тұтқырлықтың кинематикалық коэффициенті деп аталады.
|

 және
және  көлденең қималарымен шектелген ағын түтігін алайық.
көлденең қималарымен шектелген ағын түтігін алайық. 











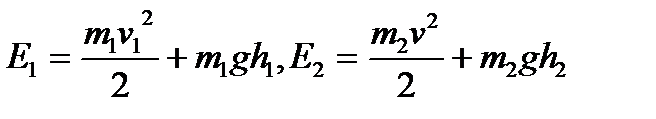 және
және 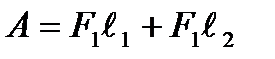 ал
ал  болса, әрі
болса, әрі  осыдан
осыдан 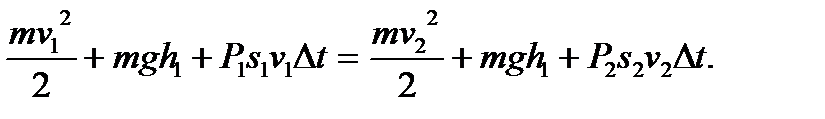 Үзілісіздік теңдеуі бойынша, сұйықтың алған көлемі
Үзілісіздік теңдеуі бойынша, сұйықтың алған көлемі  ал масса
ал масса  екенін ескерсек
екенін ескерсек
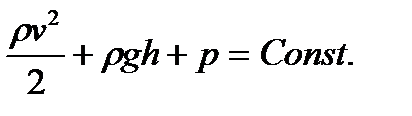
 - динамикалық қысым,
- динамикалық қысым,  - гидростатикалық қысым, р-статикалық қысым.
- гидростатикалық қысым, р-статикалық қысым. -атмосфералық қысым және
-атмосфералық қысым және 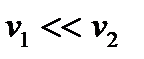 екенін ескерсек:
екенін ескерсек: немеесе
немеесе 
 деп алсақ:
деп алсақ:

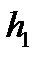
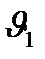
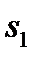





 - пропорционалдық коэффициент, ол сұйықтың тұтқырлық коэффициенті деп аталады және ол температураға байланысты. Сұйықтарда температура өскен сайын тұтқырлық азаяды, ал газдарда керісінше, температура өскен сайын тұтқырлық көбейеді.
- пропорционалдық коэффициент, ол сұйықтың тұтқырлық коэффициенті деп аталады және ол температураға байланысты. Сұйықтарда температура өскен сайын тұтқырлық азаяды, ал газдарда керісінше, температура өскен сайын тұтқырлық көбейеді.