Волновые свойства света
Такие явления, как интерференция дифракция и дисперсия света, характеризуют волновые свойства света. Дадим краткие определения этих важных характеристик.
Интерференция света Это явление наложения когерентных световых волн, в результате которого в одних местах пространства возникают максимумы, а в других минимумы интенсивности света, при этом происходит перераспределение световой энергии в пространстве. Когерентными называются световые волны, разность фаз которых остается постоянной во времени и при сложении колебаний определяет амплитуду суммарного колебания. Условие максимума интенсивности световой энергии определяется выражением
где δ — оптическая разность хода волн; λ — длина волны; к = 1, 2, 3… — целое число волн. Условие минимума интенсивности света
Радужные цвета тонких пленок, наблюдаемые на поверхности воды, покрытой тонким слоем нефти, на поверхности мыльной пленки и т. д., объясняются явлением интерференции в тонких пленках. Когда пучок параллельных лучей падает на поверхность прозрачной пленки толщиной d, свет частично отражается от этой поверхности, а, частично пройдя через пленку, отражается от второй поверхности, вновь проходит через пленку и на выходе из пленки встречается со светом отраженным от первой поверхности. В этой ситуации условия формирования максимума и минимума интенсивности света имеют вид:
где d — толщина тонкой пленки; n — коэффициент преломления пленки; r — угол преломления света в пленке. Эффект интерференции используется в фотометрии при создании узкополосных интерференционных фильтров для выделения определенной полосы длин волн в широкополосном спектре излучения.
Дифракция света Дифракцией называется явление отклонения света от прямолинейного распределения, когда свет, огибая препятствие, заходит в область геометрической тени. Распределение интенсивности света в дифракционной картине поясняется посредством метода зон Френеля. Смысл метода заключается в том, что поверхность фронта световой волны разбивается на равновеликие зоны Френеля, а окончательный результат получается сложением действия волны каждой зоны в некоторой точке О, причем учитывается.. Рассмотрим случай дифракции с помощью дифракционной решетки, представляющую собой череду узких параллельных прозрачных и непрозрачных полосок, расстояние между которыми одинаково и равно d. При наблюдении явления дифракции решетки в полихроматическом (белом) свете, где представлены различные длины волн, дифракционные максимумы для различных цветов окажутся на различных фиксированных местах, т. е. происходит разложение сложного цвета по спектру. Пусть на дифракционную решетку RR (рис. 3.3) перпендикулярно ее поверхности падает монохроматический параллельный пучок света с длинной волны λ. Свет, проходя через узкие прозрачные полоски решетки RR, испытывает дифракцию, отклоняясь во все стороны от своего начального направления.
Рис. 3.3. Интерференция в дифракционной решетке
Рассмотрим волны, распространяющиеся от решетки по направлению, составляющему угол β с нормалью к плоскости решетки. Разности хода лучей каждой прозрачной полоски, идущих от соответствующих точек отверстий, например от правых краев (точки А 1, А 2, А 3…) или от левых краев (точки B 1, B 2, B 3…), или от середины отверстий и т. д., имеют одно и тоже значение. Эти разности равны: A 2 M 1 =A 2 A 1sinβ = d sin β, A 3 M 2 =A 3 N 2 – A 2 M1 = 2 d sin β – d sin β = d sin β, A 4 M 3= A 4 N 3 – A 3 N 2 = 3 d sin β – 2 d sin β = d sin β и т.д. Для того чтобы все пучки усиливали друг друга необходимо, чтобы d sinβ равнялось целому числу длин волн λ, т. е.
где к — целое число. Таким образом, уравнение (3.17) определяет условия формирования максимумов света при длине волны λ. Это же условие позволяет определить направления, по которым будут наблюдаться максимумы света длинной волны λ:
где к = 0, ±1, ±2, ±3,… Из формулы (3.18) следует, что для любой длины волны λ можно наблюдать несколько максимумов. Направление, соответствующее к = 0, β = 0 это направление первоначального пучка. При к = 1 имеем sinβ = λ/2, при к = – 1 sinβ = –λ/2, т. е. имеются два максимума первого порядка, расположенных симметрично по обеим сторонам нулевого максимума. При к = ±2 получим sin β = ±2λ /d, т. е. два симметричных максимума второго порядка и т. д. Только при β = 0, т. е. максимумы нулевого порядка разных длин волн совпадают, а положения максимумов первого, второго и т. д. порядков различны. Чем больше длина волны λ, тем больше угол β и тем дальше первый максимум от нулевого. Если на дифракционную решетку падает полихроматический (белый) свет, и с помощью собирательный линзы проецируем источник излучения (щель) на экран, то на экране получим ряд цветных изображений источника, расположенных в порядке возрастания длин волн. На месте нулевого максимума, сходятся все длины волн, изображение источника будет белым, а по обе стороны от него развернутся цветные полосы спектра первого порядка, несколько далее цветные полосы спектра второго порядка и т. д. Так как длина волны красного цвета λ2 около 750 нм, а ультрафиолетового λ1 около 380 нм, то красный конец спектра второго порядка накладывается на спектр третьего порядка. Еще сильнее перекрываются спектры высших порядков.
l1 - длина волны ультрафиолета l2 – длина волны красного цвета 0, 1, 2,3, 4, 5 – порядок спектра Рис. 3.4 Схема дифракционного спектра На рис. 3.4 дается схематическое изображение спектра, получаемого с помощью дифракционной решетки. Благодаря дифракционной решетке, зная период решетки d можно определить длину волны λ, измерив угол β, определяющий положение максимума данного порядка:
Уменьшение периода решетки увеличивает угловое расстояние между максимумами различных длин волн, при этом, чем больше полосок имеет решетка, тем больше световой энергии проходит через нее, тем выше качество решетки. Использование дифракционной решетки в качестве монохроматора спектрофотометра рассмотрено в главе 4. Рассмотрим случай, когда поток световой энергии падает на решетку не перпендикулярно, а под углом α, когда дифракция происходит с решеткой, у которой период будет равен
Уменьшение периода решетки позволяет наблюдать дифракцию коротких длин волн. Так, поставив решетку с периодом 1 мкм под углом α = 89˚59¢40″, можно получить спектр, соответствующий решетке с периодом 0,1 нм. Этот метод дает возможность определения волн рентгеновских лучей.
Дисперсия света
Дисперсией волн называется зависимость скорости распространения волны V от длины волны λ Среды, в которых эта зависимость имеет место, называются диспергирующими Поскольку абсолютный коэффициент преломления n среды есть отношение скорости света с в вакууме к фазовой скорости V в среде
то при рассмотрении дисперсии света удобно исследовать зависимость коэффициента преломления от длины волны λ
Другими словами, дисперсия света – эта величина, определяющая скорость изменения коэффициента преломления вещества с изменением длины волны
Для прозрачных веществ коэффициент n монотонно возрастает с уменьшением длины волны λ, т. е. фиолетовые лучи преломляются сильнее красных. Это хорошо видно: если узкий пучок белого света направить на грань призмы, то на экране за призмой получим спектр цветов от красного до фиолетового. Рассмотрим некоторые примеры, поясняющие волновые характеристики света.
|

 , (2.13)
, (2.13)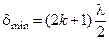 . (2.14)
. (2.14) , (2.15)
, (2.15) , (2.16)
, (2.16)
 , (3.17)
, (3.17) , (3.18)
, (3.18)
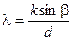 . (3.19)
. (3.19) . (3.20)
. (3.20) .(3.21)
.(3.21)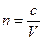 , (3.22)
, (3.22) . (3.23)
. (3.23) . (3.24)
. (3.24)


