Расчет рамы на прочность
Для расчёта рамы на прочность необходимо, чтобы выполнялись условия прочности. В качестве материала для рамы выбираем трубу D=40 мм, выполненную из стали 3СП (ГОСТ 10704-91). Рама испытывает два вида деформации – сжатие и изгиб. Определим напряжения, возникающие в обоих случаях. Сжатие Расчетная схема рамы представлена на рисунке 2.4.

Рисунок 2.4 – Расчетная схема рамы на сжатие Условием прочности является неравенство:
где
Действующее напряжение в точке сечения определяется по формуле:
где N – нормальная составляющая силы, действующей на участок рамы; А – площадь сечения трубы. Нормальная составляющая силы определяется по формуле:
где
Сила, действующая на участок рамы определяется по формуле:
где За массу установки, подвешенной на раме – примем массу установки без учета поперечных и продольных труб и опорных пластин, которая определяется по формуле:
где
Подставляя значения в (2.25), получим:
Подставляя значения в (2.24), получим:
Подставляя значения в (2.23), получим:
Площадь сечения трубы определяется по формуле:
где
Подставляя значения в (2.10), получим:
Подставляя значения в (2.22), получим:
Подставляя значения в (2.21), получим:
Условие прочности выполняется. Изгиб В качестве расчетного сечения для изгиба примем сечение рядом с поперечной балкой, т.к. изгибающий момент в нем максимален. Расчетная схема изображена на рисунке 2.5. Изгибающее напряжение в точке сечения определяется по формуле:
где М – изгибающий момент; Wx – момент сопротивления при изгибе.

Рисунок 2.5 – Расчетная схема рамы на изгиб
где
сечения. Поперечная составляющая силы определяется по формуле:
где Подставляя значения (2.8) в (2.13), получим:
Момент сопротивления при изгибе определяется по формуле:
где
Подставляя значения в (2.30), получим:
Подставляя значения (2.29) в (2.28), получим:
Подставляя значения (2.28), (2.30) в (2.27), получим:
Подставляя значения (2.27) в (2.21), получим:
Условие прочности выполняется.
|

 , (2.21)
, (2.21)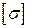 – допустимое напряжение. Для стали 3СП
– допустимое напряжение. Для стали 3СП  ;
; – действующее напряжение в точке сечения.
– действующее напряжение в точке сечения. , (2.22)
, (2.22) , (2.23)
, (2.23)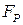 – сила действующая на участок рамы;
– сила действующая на участок рамы; - угол между силой и осью расчетного участка рамы. В расчетном случае
- угол между силой и осью расчетного участка рамы. В расчетном случае  ;
; , (2.24)
, (2.24) – масса установки, подвешенной на раме;
– масса установки, подвешенной на раме; , (2.25)
, (2.25)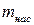 – масса насоса
– масса насоса  – масса бака
– масса бака  – масса подвесных пластин
– масса подвесных пластин  – масса опор вращения бака
– масса опор вращения бака  – масса труб верхней части рамы
– масса труб верхней части рамы  – масса обвязки (датчиков, трубопроводов и т.д.)
– масса обвязки (датчиков, трубопроводов и т.д.) 

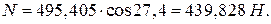
 , (2.26)
, (2.26) – наружный диаметр трубы.
– наружный диаметр трубы. 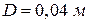 ;
; – внутренний диаметр трубы.
– внутренний диаметр трубы.  ;
; .
.

 , (2.27)
, (2.27)
 , (2.28)
, (2.28) – поперечная составляющая силы, действующей на участок рамы;
– поперечная составляющая силы, действующей на участок рамы; – плечо, равное расстоянию от поперечной силы до расчетного
– плечо, равное расстоянию от поперечной силы до расчетного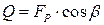 , (2.29)
, (2.29) - угол между силой
- угол между силой 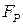 и нормалью к оси расчетного участка рамы. В расчетном случае
и нормалью к оси расчетного участка рамы. В расчетном случае  ;
;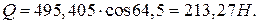
 , (2.30)
, (2.30) – наружный диаметр трубы.
– наружный диаметр трубы.  ;
; – внутренний диаметр трубы.
– внутренний диаметр трубы. 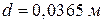 ;
;






