Біноміальний закон розподілу
Якщо ймовірність появи події у всіх незалежних випробуваннях однакова, тоді її можна знайти за формулою Бернуллі. У цьому випадку закон розподілу дискретної випадкової величини носить назву біноміального.
Закон названо біноміальним тому, що праву частину рівності (10.1) можна розглядати як загальний член розкладу бінома Ньютона
Запишемо біноміальний закон у вигляді таблиці
Монету підкинули два рази. Скласти закон розподілу дискретної випадкової величини Х – числа появи „герба”.
Рішення
Ймовірність появи „герба” при кожному киданні монети однакова і дорівнює Розглянемо всі можливі значення дискретної випадкової величини Відповідні ймовірності знайдемо за формулою Бернуллі:
Закон розподілу дискретної випадкової величини Х має вигляд
Для біноміального розподілу справедливі наступні теореми.
Доведення
Будемо розглядати дискретну випадкову величину Х – числа появи події А в п незалежних випробуваннях. Нехай:
.................................................................................
Тоді за теоремою додавання
Оскільки події є повторними, то Тоді: Іншими словами теорему можна сформулювати: математичне сподівання біноміального розподілу з параметрами п і р дорівнює добутку п·р.
Ймовірність влучення в ціль при стрільбі з гармати р=0,8. Знайти математичне сподівання загального числа влучень, якщо зроблено 5 пострілів.
Рішення
Події – влучення при кожному пострілі є незалежними і повторними, тому розподіл дискретної випадкової величини Х – числа влучень при 5 пострілах з гармати є біноміальним. Тому за формулою (10.2) знайдемо середнє число влучень
Доведення
Розглянемо дискретну випадкову величину Х – числа появи події А в п незалежних випробуваннях
Тоді, за властивістю дисперсії
де
Для знаходження складових попередньої формули, складемо розподіли
Звідси,
Тоді,
Іншими словами, дисперсія біноміального розподілу з параметрами п і р дорівнює добутку
Зроблено 10 незалежних випробувань, в кожному з яких ймовірність появи події дорівнює 0,8. Знайти дисперсію випадкової величини Х – числа появи події у цих випробуваннях.
Рішення
Знайдемо ймовірність не появи події
За формулою (10.3)
Розподіл Пуассона.
Тоді заданий таким чином закон розподілу носить назву розподілу Пуассона.
|

 Означення: Біноміальним називають розподіл ймовірностей, які визначаються за формулою Бернуллі.
Означення: Біноміальним називають розподіл ймовірностей, які визначаються за формулою Бернуллі.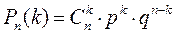 , де
, де 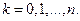 (10.1)
(10.1) .
.
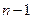


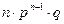
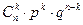
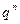
 Приклад:
Приклад: , відповідно ймовірність випадання „числа”
, відповідно ймовірність випадання „числа” 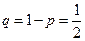 .
.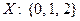 .
.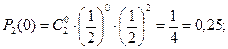


 числа появи події А в п незалежних випробуваннях дорівнює добутку числа випробувань на ймовірність появи події у кожному випробуванні
числа появи події А в п незалежних випробуваннях дорівнює добутку числа випробувань на ймовірність появи події у кожному випробуванні . (10.2)
. (10.2) - число появи події у першому випробуванні;
- число появи події у першому випробуванні; - число появи події у другому випробуванні;
- число появи події у другому випробуванні; - число появи події у
- число появи події у 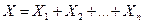 , а ймовірність появи події
, а ймовірність появи події .
.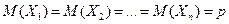 .
. , що і треба було довести.
, що і треба було довести.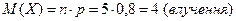 .
.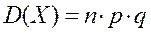 . (10.3)
. (10.3)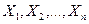 - взаємно незалежні події.
- взаємно незалежні події.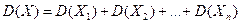 ,
,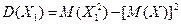 .
.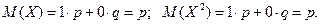
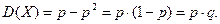
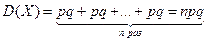 .
.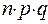 .
.
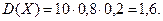
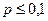 ), тоді при заданні закону розподілу для знаходження ймовірності користуються формулою Пуассона
), тоді при заданні закону розподілу для знаходження ймовірності користуються формулою Пуассона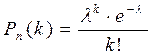 , де
, де 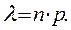 (10.4)
(10.4)


