Числові характеристики рівномірного розподілу
Ціна поділки вимірювального пристрою дорівнює 0,5 од. Показники округлюються до ближчої цілої поділки. Знайти ймовірність того, що при відрахуванні буде зроблено похибку, яка перевищує 0,01 од.
Рішення
Похибку при округленні відрахування можна розглядати як випадкову величину Х, яка має рівномірний розподіл в інтервалі між двома цілими сусідніми поділками. Довжина інтервалу за умовою задачі дорівнює 0,5
Зрозуміло, що похибка відрахування перевищить 0,01, якщо вона буде попадати в інтервал
Нормальний розподіл (розподіл Гауса)
Як видно з запису диференціальної функції, нормальний розподіл визначається двома параметрами: математичним сподіванням
Графік диференціальної функції нормального розподілу для різних значень
Рис.10.1. Графік диференціальної функції нормального розподілу
Інтегральна функція нормального розподілу згідно формули (8.7) заняття 8 буде мати вигляд
Оскільки ця функція є парною, то невизначений інтеграл від неї є непарною функцією і тому, замість інтегральної функції (13) можна використати функцію Лапласа.
|

 Математичне сподівання
Математичне сподівання
 . (10.9)
. (10.9)
 . (10.10)
. (10.10)
 Приклад:
Приклад: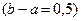 , тому за формулою (10.7)
, тому за формулою (10.7)
 . За формулою (8.6) заняття 8 знайдемо ймовірність того, що при відрахуванні буде зроблено похибку, яка перевищує 0,01 од.
. За формулою (8.6) заняття 8 знайдемо ймовірність того, що при відрахуванні буде зроблено похибку, яка перевищує 0,01 од.

 . (10.11)
. (10.11)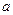 і середнім квадратичним відхиленням
і середнім квадратичним відхиленням 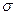 .
.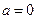 і
і 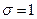 називається нормованим, його щільність (диференціальна функція) дорівнює
називається нормованим, його щільність (диференціальна функція) дорівнює (10.12)
(10.12)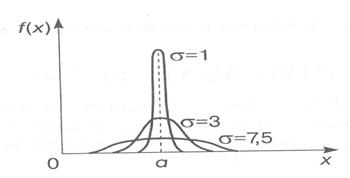
 . (10.13)
. (10.13)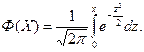 (10.14)
(10.14)


