Задачі до розділу 9.2
Випадкова величина Х задана диференціальною функцією (щільністю розподілу)
Рішення
Знайдемо дисперсію за формулою
Спочатку знайдемо математичне сподівання
Тоді дисперсія буде дорівнювати
Середнє квадратичне відхилення знайдемо за формулою
Випадкова величина Х задана диференціальною функцією (щільністю розподілу) f(x)=0,08x в інтервалі (0, 5), зовні цього інтервалу f(x)=0. Знайти дисперсію і середнє квадратичне відхилення випадкової величини Х.
Неперервна випадкова величина Х задана інтегральною функцією
Знайти математичне сподівання, дисперсію та середнє квадратичне відхилення випадкової величини Х.
Розділ 9.3. Завдання до заняття 9
1. За якою формулою обчислюється математичне сподівання неперервної випадкової величини, всі можливі значення якої належать проміжку 2. За якою формулою обчислюється математичне сподівання неперервної випадкової величини, всі можливі значення якої належать проміжку 3. Дати означення дисперсії неперервної випадкової величини. 4. За якою формулою обчислюється дисперсія неперервної випадкової величини, всі можливі значення якої належать проміжку 5. За якою формулою обчислюється дисперсія неперервної випадкової величини, всі можливі значення якої належать проміжку 6. Дати означення середнього квадратичного відхилення неперервної випадкової величини.
Розділ 10.1. Закони розподілу дискретних випадкових величин
|
Задача 9.2.1
в інтервалі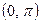 
, зовні цього інтервалу f(x)=0. Знайти дисперсію і середнє квадратичне відхилення випадкової величини Х.
.
.
.
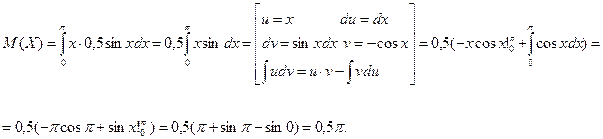
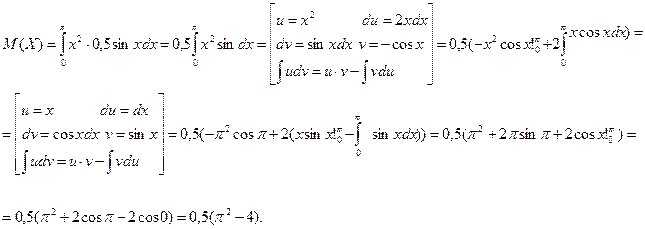
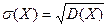
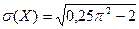Задача 9.2.2
Теоретичні питання до заняття 9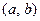
. Пояснити складові формули.
.
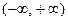