Індивідуальні завдання до розділу 6
Розділ 7.1. Доцільність введення числової характеристики розсіювання випадкової величини Досить часто зустрічаються такі випадки, коли випадкові величини мають однакові математичні сподівання, але різні можливі значення.
Дискретні випадкові величини Х та У задано наступними законами розподілу
Знайдемо математичне сподівання цих величин
Як видно, математичне сподівання приймає однакові значення, а можливі значення різні, причому дискретна випадкова величина Х має можливі значення ближчі до математичного сподівання, ніж дискретна випадкова величина У. Таким чином, за величиною математичного сподівання не можна судити про можливі значення дискретної випадкової величини, про те, як ці можливі значення розсіяні навколо математичного сподівання. Іншими словами, математичне сподівання повністю не характеризує дискретну випадкову величину Х. Тому на ряду з математичним сподіванням вводять і інші числові характеристики, що характеризують відхилення (розсіювання) випадкової величини від її середнього значення: дисперсію і середнє квадратичне відхилення. Розділ 7.2. Дисперсія дискретної випадкової величини та її властивості. Середнє квадратичне відхилення
Перед тим, як перейти до означення і властивостей дисперсії, введемо поняття відхилення випадкової величини від її математичного сподівання. Нехай Х – випадкова величина і
Доведення
Використовуючи спочатку властивість 4 математичного сподівання, а потім властивості 1 і 2 одержуємо
Тому це відхилення
Якщо врахувати означення математичного сподівання (див. формулу 6.2), то вираз для дисперсії
Формула (7.1) незручна при обчисленнях, тому перетворимо її і подамо у більш зручному вигляді. Для цього застосуємо теорему.
Доведення Із означення дисперсії випливає
Оскільки
отримаємо далі
Таким чином, остаточно отримуємо
де
1. Знайти дисперсію випадкової величини, заданої законом розподілу
Рішення Знайдемо спочатку математичне сподівання випадкової величини Х
Тепер знайдемо математичне сподівання квадрата випадкової величини, для цього складемо розподіл
За формулою (7.3) маємо
Властивість 1. Дисперсія сталої величини дорівнює нулю
Доведення
За формулою (7.3) маємо
Властивість 2. Сталий множник можна виносити за знак дисперсії, піднісши його до квадрата, тобто
Доведення
За означенням дисперсії маємо
Властивість 3. Дисперсія суми двох випадкових величин дорівнює сумі дисперсії цих величин, тобто
Доведення За формулою (7.3) маємо
Властивість 4. Дисперсія суми випадкової величини і сталої дорівнює дисперсії випадкової величини
Доведення Використаємо властивості 1 і 3 дисперсії
Властивість 5. Дисперсія різниці двох випадкових величин дорівнює сумі дисперсій цих випадкових величин
Доведення Відповідно до властивостей 2 і 3 маємо:
|

 Приклад:
Приклад:
 - її математичне сподівання. Розглянемо як нову випадкову величину різницю
- її математичне сподівання. Розглянемо як нову випадкову величину різницю  . Відхиленням називається різниця між випадковою величиною та її математичним сподіванням.
. Відхиленням називається різниця між випадковою величиною та її математичним сподіванням. Теорема: Математичне сподівання відхилення випадкової величини від її математичного сподівання дорівнює нулю, тобто
Теорема: Математичне сподівання відхилення випадкової величини від її математичного сподівання дорівнює нулю, тобто
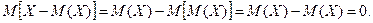

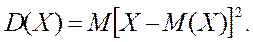 (7.1)
(7.1) із формули (7.1) можна записати у розгорнутому вигляді так
із формули (7.1) можна записати у розгорнутому вигляді так (7.2)
(7.2) (7.3)
(7.3) .
. і
і  , то ввівши позначення
, то ввівши позначення (7.4)
(7.4)
 ,
, 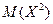 – математичне сподівання квадрата випадкової величини, знаходиться за формулою (7.4), а
– математичне сподівання квадрата випадкової величини, знаходиться за формулою (7.4), а 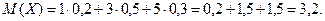


 .
.
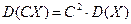 .
. .
. .
.
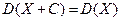 .
.
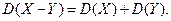

 . (7.5)
. (7.5)


