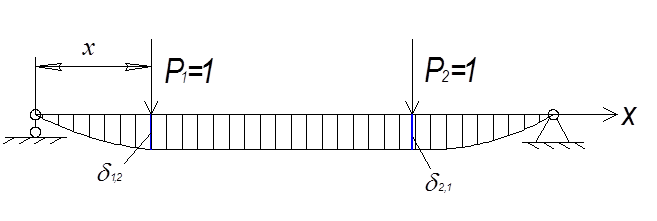Определение продольных усилий, действующих в стержнях фермы с помощью линий влияния
Ординаты линий влияния, находящиеся под грузами, для всех стержней фермы приведены в табл.1. Таблица 1 Ординаты линий влияния
Определение максимальных значений продольных усилий Для этого нужно поместить подвижные грузы с их наибольшим значением в наиболее невыгодное положение (рис. 45 а), используя линии влияния. Расчетное значение определяется по формуле (18). Стержень 0-1
Стержень 1-3
Стержень 0-2
Стержень 2-4
Стержень 1-4
Стержень 1-2
Стержень 3-4
Определение минимальных значений продольных усилий
Поместим подвижные грузы с их наименьшим значением в наиболее благоприятное положение (рис. 45 б). Расчетное значение определяется также по формуле (18). Стержень 0-1
Стержень 1-3
Стержень 0-2
Стержень 2-4
Стержень 1-4
Стержень 1-2
Стержень 3-4
Линии влияния перемещений Общие положения Для суждения о жесткости конструкции определяют перемещения отдельных ее точек или сечений. Эта операция довольно трудоемка особенно при громоздкой нагрузке, необходимости расчета при различных вариантах нагрузки или наличии подвижных нагрузок. В этих случаях для определения необходимых перемещений целесообразно использовать их линии влияния. Линия влияния перемещения какой-либо точки или сечения конструкции представляет собой график, выражающий закон изменения этого перемещения в зависимости от положения единичного груза, перемещающегося по конструкции и сохраняющего неизменное направление. Для каждой рассматриваемой точки или сечения конструкции строится своя линия влияния. С помощью построенной линии влияния искомое перемещение определяется по формуле:
Общее правило построения линий влияния перемещений аналогично правилу построения линий влияния (п.1.4.). Линию влияния перемещения можно построить, выполняя последовательно следующие операции: - выбрать систему координат с осями x и δ;. Начало координат по соображениям, изложенным в п. 1.4, целесообразно выбирать на левом конце расчетной схемы конструкции; - ось x – ось абсцисс точки приложения единичного груза, условимся направлять ее вправо; - ось δ; – ось ординат линии влияния перемещения δ;, условимся направлять ее вниз; - единичный груз поставить в произвольное положение и обозначить координату «x» его точки приложения. При этом все действующие на конструкцию нагрузки удаляются, т.е. конструкция рассматривается загруженной только единичным грузом; - считая единичный груз неподвижным в выбранном произвольном положении, определить искомое перемещение, вызванное этим грузом, любым из способов, рассматриваемых в курсах сопротивления материалов и строительной механики. При этом перемещение выразится некоторой формулой, содержащей «x». Эта формула будет представлять собой уравнение линии влияния, если считать в ней «x» переменным. Обычно единичный груз приходится ставить в произвольное положение поочередно на нескольких участках. Для каждого участка получится свое уравнение линии влияния, справедливое только для этого участка (включая его границы). Границами участка являются границы конструкции, точки (сечения), для которых строится линия влияния перемещения, точки приложения опорных реакций от единичного груза. Линия влияния перемещения изображается кривой линией, для более или менее точного построения которой требуется определить сравнительно много ординат. Поэтому можно ограничиться составлением уравнения линии влияния на отдельных ее участках и по нему определять требуемые ординаты и площади для формулы (19). Иногда вместо непосредственного построения линии влияния перемещения по правилу, изложенному выше, целесообразно находить равнозначную ей другую линию, используя для этого принцип взаимности перемещений.
Пусть требуется построить линию влияния вертикального перемещения δ2,1 точки 2, вызванного единичным грузом P1=1, перемещающимся по балке и приложенным в точке 1, координата «x» которого переменна. Приложим в точке 2 добавочную вертикальную силу P2=1. Эта сила вызывает вертикальное перемещение δ1,2 точки 1. На основании принципа взаимности перемещений имеем δ2,1 = δ1,2. Следовательно, вместо непосредственного определения перемещений рассматриваемой точки 2 от подвижного единичного груза P1=1 можно определять перемещения δ1,2 точки 1, вызванные добавочной силой P2=1, приложенной в рассматриваемой неподвижной точке 2. Перемещение δ1,2 представляет собой прогиб балки в точке 1, вызванный добавочной силой P2=1, приложенной в рассматриваемой точке 2. Заметим, что роль точки 1 играют все точки приложения единичного груза P1=1 при его движении по балке (т.е. все точки оси балки). Отсюда следует, что линия влияния искомого перемещения точки 2 представляет собой линию прогибов балки (т.е. линию изогнутой оси балки) от добавочной единичной силы P2=1, приложенной в рассматриваемой неподвижной точке 2. Уравнение линии влияния представляет собой уравнение изогнутой оси балки от добавочной силы P2. Уравнение же изогнутой оси балки находится путем интегрирования ее дифференциального уравнения. В общем случае принцип взаимности перемещений справедлив при любых направлениях сил P1 и P2. При этом перемещения δ1,2 и δ2,1 направлены по направлению соответственно сил P1 и P2 (точнее это есть проекции полных линейных перемещений точек 1 и 2 на направления приложенных в этих точках сил). Изложенное выше применение принципа взаимности перемещений для построения линий влияния относится ко всем линейно деформируемым системам-балкам, фермам, рамам и т.д. При построении линий влияния угловых перемещений (углов поворота) сечения следует вместо добавочной единичной сосредоточенной силы P2 приложить в рассматриваемом сечении пару сил с моментом M2=1 (единичный момент). Рассмотрим построение линий влияния вертикальных перемещений сечений балки и узлов фермы.
|

 т
т т
т


 т
т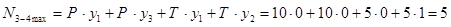 т
т т
т т
т


 т
т т
т . (19)
. (19)