Характер линий влияния при движении единичного груза понизу и поверху фермы
Характер линий влияния при движении единичного груза понизу или поверху зависит от характера решетки фермы. В фермах с треугольной решеткой (без вертикальных стержней) линии влияния для всех стержней изменяются от движения единичного груза понизу или поверху. Характер линии влияния для различных стержней таких ферм показан на рис. 36. Рассмотрим стержни 1-3,1-2, 5-7, 4-6, 5-6. Единичный груз перемещается поверху (Р обозначено штрихом) Стержень 1-3. Рассекаем ферму сечением I-I. Поочередно рассматриваем в равновесии левую и правую части фермы. Моментной точкой является точка 2. Единичный груз находится слева от точки 2, в равновесии – правая часть фермы.
Отсюда
Это уравнение справедливо при 0 £ x £ d: при x = 0 N1-3 = 0; при x = d Единичный груз находится справа от моментной точки 2, в равновесии – левая часть фермы.
Отсюда
Уравнение справедливо при d £ x £ l: при x = d при x = 0 N1-3 = 0. Линия влияния N1-3 изображена в виде треугольника АВ'С (рис. 36 а). Стержень 1-2. Для этого стержня моментной точки нет. Возьмем проекцию усилия в этом стержне на ось Z. Уравнение равновесия правой части фермы имеет вид
Отсюда
Уравнение справедливо при - ∞ £ x £ 0: при x = 0 Уравнение равновесия левой части фермы имеет вид
Отсюда
Уравнение справедливо при d £ x £ l: при x =d при x = l Линия влияния АВ'С (рис. 36 б)
Стержень 5-7. Рассекаем ферму сечением II-II на две части. Для этого стержня моментной точкой является точка 6. Уравнение равновесия правой части фермы имеет вид 
Рис. 36
Уравнение справедливо при 0 £ x £ 5d: при x = 0 Уравнение равновесия левой части фермы имеет вид
Уравнение справедливо при 5d £ x £ l: при x = 5d Линия влияния АВ'Д (рис. 36 в).
Стержень 4-6. Моментной точкой для стержня 4-6 является точка 5. Уравнение равновесия правой части фермы имеет вид
При движении единичного груза поверху можем пользоваться левым отрезком линии влияния лишь до узла 4, а правым – до узла 6. Поэтому пределы для вышезаданного равенства будут 0 £ x £ 3d.
При x = 0 при x = 3d, Уравнение равновесия левой части фермы имеет вид
Отсюда
Уравнение действительно при 5d £ x £ l: при x = 5d Линия влияния АВС'Д (рис. 36 г).
Стержень 5-6. Уравнение равновесия правой части фермы. Берем проекцию усилий на
Отсюда
Уравнение действительно при 0 £ x £ 3d: при x = 0 Уравнение равновесия левой части фермы имеет вид
Отсюда
Уравнение действительно при 5d £ x £ l: при x = 5d Линия влияния АВ'С'Д (рис. 36 д). Единичный груз перемещается понизу (Р обозначено сплошной линией) Стержень 1-3. Единичный груз слева от точки 2. Моментная точка 2. Уравнение равновесия правой части фермы имеет вид
Отсюда
Уравнение действительно при - ∞ £ x £ 0: при x = 0 Единичный груз справа от точки 2.
Отсюда
Уравнение действительно при 2d £ x £ l: при x =2d при x = l Линия влияния АВС (рис. 36 а).
Стержень 1-2. Единичный груз слева от точки 2 Уравнение равновесия правой части фермы будет иметь вид
Отсюда
Уравнение действительно при - ∞ £ x £ 0: при x = 0 Единичный груз справа от точки 2. Уравнение равновесия левой части фермы будет иметь вид
Отсюда
Уравнение действительно при 2d £ x £ l: при x = 2d Линия влияния АВС (рис. 36 б).
Стержень 5-7. Моментная точка 6. Единичный груз слева от точки 6. Уравнение равновесия правой части фермы будет иметь вид
Отсюда
Уравнение действительно при 0 £ x £ 4d: при x = 0 при x = 4d Единичный груз справа от точки 6. Уравнение равновесия левой части фермы будет иметь вид
Отсюда
Уравнение действительно при 6d £ x £ l: при x = 6d при x = l Линия влияния АВСД (рис. 36 в). Стержень 4-6. Моментная точка 5. Единичный груз слева от точки 5. Уравнение равновесия правой части фермы будет иметь вид
Отсюда
Уравнение действительно при 0 £ x £ 4d: при x = 0 при x = 4d Единичный груз справа от точки 5. Уравнение равновесия левой части фермы будет иметь вид
Отсюда
Уравнение действительно при 4d £ x £ l: при x = 4d при x = l Линия влияния АСД (рис. 36 г).
Стержень 5-6. Единичный груз слева от сечения II-II. Уравнение равновесия правой части фермы будет иметь вид
Отсюда
Уравнение действительно при 0 £ x £ 4d: при x = 0 при x = 4d Единичный груз справа от сечения II. Уравнение равновесия левой части фермы будет иметь вид
Отсюда
Уравнение действительно при 6d £ x £ l: при x = 6d при x = l Линия влияния АВСД (рис. 36 д). Если ферма имеет решетку с вертикальными стержнями (стойками), то линии влияния для стержней поясов и раскосов остаются неизменными при движении единичного груза понизу или поверху. Изменяются только линии влияния для стоек. Такими фермами являются фермы с раскосной решеткой (см. рис. 24 а) и треугольной решеткой с дополнительными стойками (см. рис. 24 г). Характер линий влияния для различных стоек этих ферм показан на рис 37. Рекомендуется самостоятельно разобрать линии влияния на рис. 37 на основании общих положений, рассмотренных ранее.
Рис. 37
|

 .
. .
. .
.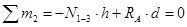 .
. .
. ;
; .
. .
. .
. ,
, .
. ,
, . Отсюда
. Отсюда  .
. , при x = 5d
, при x = 5d  .
. . Отсюда
. Отсюда  .
. ; при x = l
; при x = l 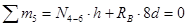 .
. .
. ,
, .
. .
. .
. ; при x = l
; при x = l  .
. .
. ; при x =3d
; при x =3d  .
. .
. .
. , при x = l
, при x = l  .
. .
. .
. .
. ,
, .
.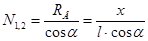 .
. .
. .
. ; при x = l
; при x = l 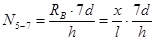 .
. .
.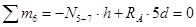 .
. .
. ,
, .
. .
. .
. .
. ,
, .
. .
.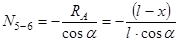 .
. ,
,



