Линия влияния продольного усилия для стойки 9-10
Для этой стойки нет сквозного сечения, пересекающего три стержня. Следует воспользоваться вырезанием узла. Целесообразно вырезать узел 10 (рис. 35). Пусть единичный груз движется понизу (рис. 35 б). При любом положении единичного груза на нижнем поясе уравнение равновесия вырезанного узла 10 (рис. 35 а) будет иметь вид
Отсюда получится уравнение линии влияния
Казалось бы, линия влияния должна иметь один участок. Однако это не так.
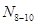 и и 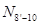 , которые также зависят от положения единичного груза на нижнем поясе. Следовательно, характер линии влияния , которые также зависят от положения единичного груза на нижнем поясе. Следовательно, характер линии влияния 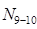 зависит от характера линий влияния зависит от характера линий влияния 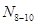 и и 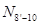 (см. п.3.2.2). Поэтому необходимо установить участки, линии влияния (см. п.3.2.2). Поэтому необходимо установить участки, линии влияния 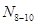 и и 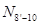 , для каждого из них определить значения , для каждого из них определить значения 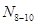 и и 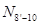 при произвольном положении единичного груза на участке, подставить эти значения в уравнение (17), в результате чего получится уравнение линии влияния при произвольном положении единичного груза на участке, подставить эти значения в уравнение (17), в результате чего получится уравнение линии влияния 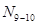 для каждого участка, определяемого характером линии влияния для каждого участка, определяемого характером линии влияния 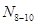 и линии влияния и линии влияния 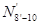 . .
Такое решение оказывается очень громоздким. Лучше в данном случае построить линию влияния без составления ее уравнений для упомянутых участков. Из уравнения (17) следует, что любая ордината линии влияния Линии влияния
где 1,15 – ординаты линии влияния Пусть теперь единичный груз перемещается поверху. Линия влияния Когда единичный груз находится на левом и правом участках, т.е. за пределами разрезанных панелей пояса, уравнение равновесия узла 10 будет таким же, как и при движении единичного груза понизу, и любая ордината линии влияния Для построения линии влияния N 9-10 при x = 4d= N 9-10 при x = 6d = где –0,92 – ординаты линий влияния Составлять уравнение линии влияния
Отсюда искомая ордината линии влияния
Соединив точки линии влияния
|

 .
.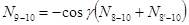 (17)
(17)

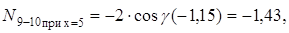
 .
. =1,14,
=1,14, .
. .
.


