Линия влияния продольных усилий стойки 3-4
Для стойки 3-4 нет сквозного сечения, пересекающего три стержня. Следует воспользоваться вырезанием узла. Характерной особенностью этой стойки является то, что в узле 3 сходятся кроме нее еще два стержня нижнего пояса, оси которых направлены по одной прямой. Вырезать следует именно этот узел (рис. 34). Стойка окажется так называемым единичным стержнем в трехстержневом узле. Пусть единичный груз перемещается понизу (рис. 34 а). В этом случае линия влияния будет иметь четыре участка (см. п. 3.2.2, первый вариант): слева и справа от разрезанных панелей 1-3 и 3-5 и два участка в пределах этих панелей.

Рис. 34
Помещая единичный груз поочередно слева и справа от разрезанных панелей, получим одно и то же уравнение равновесия вырезанного узла 3 (рис. 34 б): Оно будет и уравнением линии влияния При построении линии влияния в пределах разрезанных панелей 1-3 и 3-5 единичный груз следует перемещать по жестким балочкам, опирающимся на узлы этих панелей (см. п. 3.2). Пусть единичный груз находится в произвольном положении в пределах панели 1-3 (рис. 34 в). Вместо него на ферму действуют его составляющие Уравнение равновесия вырезанного узла 3 будет иметь вид
Отсюда Это уравнение л.в. Соединив эти точки прямой, получим линию влияния Аналогично получается линия влияния Можно не составлять уравнения линии влияния Поставить единичный груз в узел 3 (рис. 34 г). Тогда уравнение равновесия этого узла будет иметь вид
Отсюда значение ординаты линии влияния Следовательно: при x = d при x = 3d при x = 2d Соединив эти точки прямыми линиями, получим линии влияния При перемещении единичного груза по верхнему поясу при любом его положении уравнение равновесия вырезанного узла будет иметь вид
Это уравнение будет и уравнением линии влияния Итак, когда стойка является одиночным стержнем в трехстержневом узле, усилие в ней возникает только тогда, когда единичный груз находится в пределах, примыкающих к ней панелей пояса. Линия влияния имеет очень простой, легко запоминающийся вид. Нет необходимости составлять рассмотренные выше уравнения линий влияния, а строить их без этих уравнений.
|



 .
. для участков слева (0 £ x £ d) и справа (3d £ x £ l) от разрезанных панелей. Из него следует, что пока единичный груз находится за пределами примыкающих к стойке 3-4 панелей 1-3 и 3-5 нижнего пояса, по которому перемещается единичный груз, усилие в нем равно нулю.
для участков слева (0 £ x £ d) и справа (3d £ x £ l) от разрезанных панелей. Из него следует, что пока единичный груз находится за пределами примыкающих к стойке 3-4 панелей 1-3 и 3-5 нижнего пояса, по которому перемещается единичный груз, усилие в нем равно нулю. и
и  , одна из которых (
, одна из которых ( .
.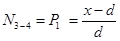 .
. .
.


