О построении линий влияния усилий без составления их уравнений

Рассмотренная выше методика построения линий влияния для балок и ферм позволяет установить характер линий влияния для усилий в сечениях балки и стержнях фермы, их характерные особенности. Если все это хорошо усвоить, то линии влияния можно строить без составления их уравнений. Эти уравнения при практическом использовании линий влияния для определения усилий от реальной нагрузки не требуются, т.к. линии влияния изображаются отрезками прямых линий. Все необходимые их ординаты легко определяются из геометрических соображений (см. примеры в п. 3.5).

Для построения линий влияния без составления уравнений необходимо:

- установить границы отдельных участков линии влияния (см. п.п. 2.2; 3.2.1; 3.2.2);

- определить ординаты линий влияния на границах участков, помещая в граничные точки поочередно единичный груз (вспомним: ордината линий влияния равна искомому усилию от единичного груза, когда он находится над этой ординатой);

- соединить концы ординат отрезками прямых линий, в результате чего и получится линия влияния.

Рассмотрим для примера построение линий влияния для стержней 7-9, 8-9 (рис. 28) при движении единичного груза понизу.

 

Линия влияния N_7-9

Замечаем, что можно воспользоваться сквозным сечением, разрезающим стержни 7-9, 8-9, 8-10. Моментной точкой для стержня 7-9 является точка 8. Ее проекция находится в узле 7 разрезанной панели 7-9 пояса, по которому перемещается единичный груз.

Следовательно, линия влияния имеет два участка и изображается прямыми, пересекающимися под моментной точкой. Границы участков: точки 0 и 7 для левого участка, точки 7 и для правого участка.

Легко установить, что ординаты линий влияния в точках 0 и n равны нулю (единичный груз, помещенный в эти точки, полностью воспринимается опорами фермы).

Определим ординату линий влияния под узлом 7, т.е. под моментной точкой 8. Для этого устанавливаем единичный груз в точке 7, мысленно рассекаем ферму упомянутым выше сечением и отбрасываем левую часть. Из условия равновесия правой части () находим искомую ординату в точке 7

,

где - реакция опоры «n», когда единичный груз находится в точке 7 (x = 4d).

Линия влияния N_7-9 изображена на рис. 28.

 

Линия влияния N_8-9

При построении линии влияния N_8-9 можно воспользоваться тем же сквозным сечением, что и для стержня 7-9. Моментной точкой является точка «m», находящаяся за пределами разрезанной панели 7-9 пояса, по которому перемещается единичный груз. Значит линия влияния имеет три участка: слева и справа от разрезанной панели 7-9 и в пределах этой панели.

Границы участков: точки 0 и 7 – для левого участка, точки 9 и n – для правого участка, точки 7-9 – для переходного участка в пределах разрезанной панели. Используемое сечение пересекает непараллельные пояса, значит прямые, изображающие левый и правый участки, пересекаются под моментной точкой «m».

Переходная прямая между левым и правым участками наклонена в сторону, противоположную раскосу 8-9 (перекрещивается с ним).

Определим ординаты линии влияния на границах участков.

Под опорными узлами 0 и n они равны нулю.

Поставим единичный груз в точку 7, мысленно разрезаем ферму упомянутым сквозными сечением и отбрасываем левую часть. Из условия равновесия правой части () находим ординату линии влияния под узлом 7 в точке 7

,

где - реакция опоры «n», когда единичный груз находится в точке 7 (x = 4d).

Поставив единичный груз в точку 9, мысленно разрезаем ферму упомянутым сквозным сечением и отбрасываем правую часть. Из условия равновесия левой части найдем ординату линии влияния под узлом 9 в точке 9

,

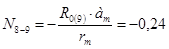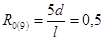где - реакция опоры «0», когда единичный груз находится в точке 9 (x = 5d).

Линия влияния N_8-9 изображена на рис. 28.