Линия влияния для стоек
Это стержни 1-2 и 3-4. Стойка 1-2 Ферму рассекаем сечением III-III и находим моментную точку к (рис. 50).
а) б) Рис. 50
Перемещаем груз по правой части фермы. В равновесии рассматриваем левую часть фермы (рис. 50 а).
отсюда
Это уравнение справедливо на участке При x = l при x = Перемещаем груз по левой части фермы. В равновесии рассмотрим правую часть фермы (рис. 52 б).
отсюда
Это уравнение справедливо на участке -∞ £ x £ 0. При x = 0 Линия влияния N1-2 показана на рис. 45.
Стойка 3-4 Для этой стойки нет сечения. Воспользуемся методом вырезания узла (рис. 51). Линия влияния будет иметь четыре участка: (0… Помещая груз Р = 1 поочередно слева и справа от разрезанных панелей, получим уравнение равновесия вырезанного узла 3 (рис. 51 а):
а) б) Рис. 51
Это и есть уравнение линии влияния Следовательно, пока единичный груз находится за пределами примыкающих к стойке 3-4 панелей 1-3 и 3-5 нижнего пояса, усилие в ней равно нулю, т.е. стойка 3-4 не нагружена. Теперь поставим единичный груз в узел 3 (рис 51 б). Тогда уравнение равновесия этого узла будет иметь вид:
Уравнение справедливо на участках Отсюда при x = Линия влияния N1-4 показана на рис. 45.
|
,
.
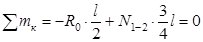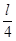£ x £ l.
= 0,
.
,
.
); (
); (
.
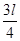для участков слева (0 £ x £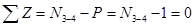 
.
