Пример определения перемещения узла фермы с помощью линии влиянияДля определения перемещения узла фермы используется известная формула:
где Ni – усилие в i-ом стержне от приложенной к ферме нагрузки; Ni0 – усилие в i ‑ом стержне от добавочной единичной силы, приложенной в рассматриваемом узле по направлению искомого перемещения; Li, Fi, Ei – соответственно длина (по расчетной схеме фермы), площадь поперечного сечения и модуль упругости материала i -го стержня; n – число стержней в ферме. По этой формуле можно определить искомое перемещение узла фермы, не пользуясь его линией влияния.
Таблица 2 Параметры для определения перемещения в узле 9 фермы
Однако целесообразно все же воспользоваться линией влияния, особенно при необходимости изучения влияния нескольких вариантов нагружения фермы и при наличии подвижной нагрузки. При построении линии влияния перемещения некоторого узла фермы в качестве фактически приложенной к ферме нагрузки принимается единичный сосредоточенный груз, который перемещается по одному из ее поясов (он вызывает в стержнях усилие Ni). Добавочная единичная сила прикладывается в рассматриваемом узле по направлению искомого перемещения (она вызывает усилие Ni0). Усилия Ni и Ni0 целесообразно определять с помощью линий влияния усилий в стержнях фермы (для каждого стержня должна быть построена эта линия влияния). Поскольку и единичный груз, и добавочная сила являются единичными силами, то процессы построения линий влияния перемещения по общему правилу и с использованием принципа независимости перемещений будут одинаковыми, различаясь только по смыслу. Любую нагрузку фермы можно представить приложенной в узлах. Поэтому нет необходимости находить уравнение линии влияния перемещения. Достаточно определить ее ординаты под узлами, помещая в них поочередно единичный подвижный груз. В этом случае линия влияния перемещения изобразится приближенно ломаной линией с вершинами под узлами фермы. Пример. Определить вертикальное перемещение δ9 узла 9 фермы, изображенной на рис. 55 а, с помощью его линии влияния. Все стержни фермы имеют одинаковые площади сечения F и изготовлены из одного материала с модулем упругости E. P1 = P2 = P3 = P4 = P.
Решение Построение линии влияния δс. Нагрузка приложена к ферме вертикально в узлах 3, 5, 7, 9 нижнего пояса. При построении линии влияния ограничимся определением ее ординат под этими узлами, помещая в них поочередно единичный подвижный груз, а добавочную силу всякий раз прикладывая в узле 9 (рис. 55 в). Единичный груз и добавочную силу направляем вертикально вниз. Рассмотрим порядок вычисления ординат линии влияния δ9 под узлом 3. Приложим единичный груз в узле 3 и определим вызванное им усилие Ni во всех стержнях фермы с помощью их линий влияния, изображенных на рис. 55 б. Приложим добавочную единичную силу в узле 9 и определим вызванные ею усилия Ni0 во всех стержнях с помощью тех же линий влияния. Определим ординату линии влияния под узлом 3 (обозначим ее y3) по формуле:
В таком же порядке определяются ординаты линии влияния δ9 под остальными узлами. Их определение представлено в табл. 2. Линия влияния δ9 изображена на рис. 55 г.
|
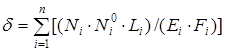, (20)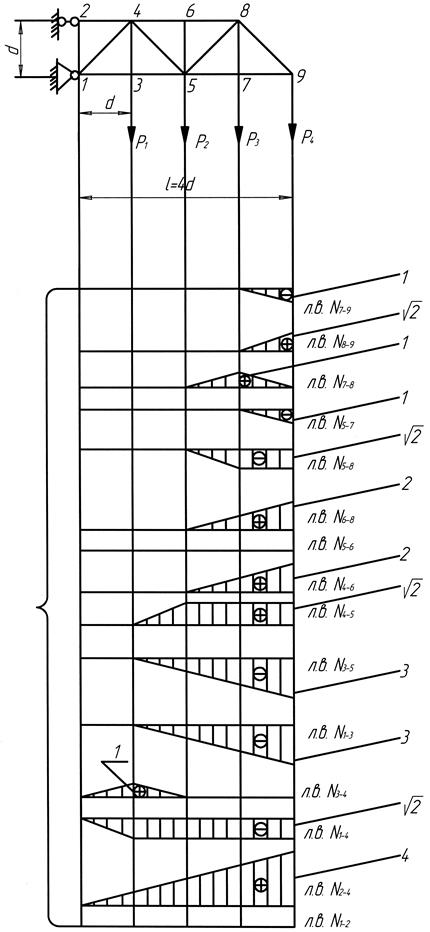
.
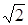
