Постановка задачи минимизации. Определения
Пусть f(x) – действительная функция одной переменной, определенная на множестве Х Точка Точка Существуют различные постановки задачи минимизации. В самой широкой постановке требуется найти все точки локального минимума и отвечающие им значения f(x). В приложениях чаще всего возникает задача вычисления конкретной точки локального минимума или точки глобального минимума. Иногда представляет интерес только лишь минимальное значение целевой функции, независимо от того, в какой именно точке оно достигается. Чтобы применить один из алгоритмов минимизации, следует предварительно найти отрезок локализации. Отрезок локализации – это отрезок, содержащий точку Унимодальные функции. Пусть f(x) – функция, определенная на [ A, B ]. Функция называется унимодальной, если на [ A, B ] существует единственная точка Для унимодальных функций справедливы следующие утверждения: Утверждение 1. Если для всех х Î [ A, B ] выполнено условие f” (х) > 0, то функция унимодальна на отрезке [ A, B ]. Утверждение 2. Пусть f(х) – унимодальная функция на [ A, B ] и 1) если f (a) £ f (b), то 2) если f (a) ³ f (b), то 3) если f (a) ³ f (g) и f (g) £ f (b), то Утверждение 3. Если функция унимодальна на [ A, B ], то она унимодальна и на любом [c, d ] Î [ A, B ]. Далее приведём наиболее распространённые методы решения задачи одномерной минимизации.
|

 .
. называется точкой глобального минимума функции f на множестве Х, если для всех
называется точкой глобального минимума функции f на множестве Х, если для всех 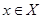 выполняется неравенство
выполняется неравенство 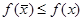 .
. , на котором она является единственной точкой локального минимума.
, на котором она является единственной точкой локального минимума. локального минимума функции f(x), причем функция f(x) строго убывает при х £
локального минимума функции f(x), причем функция f(x) строго убывает при х £  . Тогда:
. Тогда:


