Покоординатный спуск
В методе покоординатного спуска в качестве очередного направления спуска выбирают направление одной из координатных осей. Наиболее известным является метод циклического покоординатного спуска. Опишем очередной (n + 1)-й цикл одного из вариантов этого метода, считая приближение x ( n ) уже найденным. Цикл с номером n + 1 состоит из m шагов. На первом шаге производят спуск по координате х 1. Значения х 2 = х 2( n ), …,
Фактически решается задача минимизации функции одной переменной
На втором шаге производят спуск по координате х 2. Значения х 1 = х 1( n +1), х 3 = х 3( n ), …, хm = хm ( n ) остальных координат фиксируют и х 2( n+ 1) выбирают как решение задачи одномерной минимизации
Аналогично осуществляют остальные шаги. В результате получается очередное приближение x ( n +1) к точке минимума. Далее цикл метода снова повторяют. На рис.3.2 изображена геометрическая иллюстрация циклического покоординатного спуска для m =2.
Рисунок 3.2 - Геометрическая иллюстрация циклического покоординатного спуска Приведём блок-схему алгоритма основной программы метода циклического покоординатного спуска для m =2 (рис.3.3).
Начало
   < Eps < Eps
Рисунок 3.3 - Блок-схема алгоритма основной программы метода циклического покоординатного спуска для функции двух переменных F(x, y) – заданная целевая функция – должна быть описана отдельно. Входные данные: Х0, ХN, Y0, YN – граничные значения переменных x и y; Eps – заданная точность вычислений; Результаты: X, Y - приближение к искомым значениям координат точки минимума; F(X,Y) – значение целевой функции в точке минимума.
На рис.3.4 приведена блок-схема алгоритма процедуры MINX, осуществляющая поиск значения переменной Х, при котором целевая функция F(x, y) принимает наименьшее значение при фиксированном значении переменной Y. В данном примере в процедуре MINX для решения одномерной задачи минимизации используется метод дихотомии. Входные параметры: А, B – границы изменения значений переменной Х; Eps – заданная точность вычислений; Выходные параметры: XМ - приближение к искомому значению X точки минимума;
MINX (A, B, Eps, Y, XM)
   Alfa = (A + B)/2 – Eps/3 Alfa = (A + B)/2 – Eps/3
      FA £ FB FA £ FB
XM = (A + B)/2
Рисунок 3.4 - Блок-схема алгоритма процедуры MINX Аналогично, для поиска значения переменной Y, при котором целевая функция F(x, y) принимает наименьшее значение при фиксированном значении переменной X, составляется блок-схема алгоритма процедуры MINY (рис.3.5). Входные параметры: А, B – границы изменения значений переменной Y; Eps – заданная точность вычислений; Выходные параметры: YМ - приближение к искомому значению Y точки минимума;
MINY (A, B, Eps, X, YM)
   Alfa = (A + B)/2 – Eps/3 Alfa = (A + B)/2 – Eps/3
      FA £ FB FA £ FB
YM = (A + B)/2
Рисунок 3.5 - Блок-схема алгоритма процедуры MINY
|

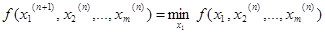 .
.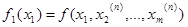 .
. .
.


 Ввод Х0, ХN, Y0, YN, Eps
Ввод Х0, ХN, Y0, YN, Eps


 Y1 = Y
Y1 = Y

 MINX(X0, XN, Eps, Y1, X)
MINX(X0, XN, Eps, Y1, X)
 +
+ Вывод (X, Y), F(X, Y)
Вывод (X, Y), F(X, Y)
 end
end






 +
+
 end
end


