Рельеф функции
Основные трудности многомерного случая удобно рассмотреть на примере функции двух переменных Ф(х, у). Она описывает некоторую поверхность в трёхмерном пространстве с координатами х, у, Ф. Задача Ф(х, у) = min означает поиск низшей точки этой поверхности. Множество точек, для которых целевая функция принимает постоянное значение f( x ) = c, называется поверхностью уровня. В случае m = 2 это множество называют линией уровня. Как в топографии, изобразим рельеф поверхности Ф(х, у) линиями уровня. Проведём равноотстоящие плоскости Ф = const и найдём линии их пересечения с поверхностью Ф(х, у); проекции этих линий на плоскость х, у называют линиями уровня. Полученная картина напоминает топографическое изображение рельефа горизонталями. По виду линий уровня условно выделим три типа рельефа: котловинный, овражный и неупорядоченный. При котловинном рельефе линии уровня похожи на эллипсы (рис. 3.1, а). В малой окрестности невырожденного минимума рельеф функции котловинный. В самом деле, точка минимума гладкой функции определяется необходимыми условиями
и разложение функции по формуле Тейлора вблизи минимума имеет вид
причём квадратичная форма (3.2) – положительно определённая, иначе эта точка не была бы невырожденным минимумом. А линии уровня знакоопределённой квадратичной формы – это эллипсы.
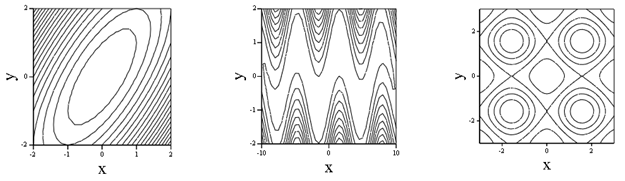 Рисунок 3.1 - Типы рельефа: а) котловинный, б) овражный и в) неупорядоченный Рисунок 3.1 - Типы рельефа: а) котловинный, б) овражный и в) неупорядоченный
Отметим, что условию (3.1) удовлетворяют также точки максимумов и седловые точки. Но в точках максимумов квадратичная форма (3.2) – отрицательно определённая, а в седловинах она знакопеременна. Рассмотрим овражный тип рельефа. Чаще линии уровня всюду гладкие, но на них имеются участки с большой кривизной; геометрические места точек с наибольшей кривизной назовём разрешимыми оврагами или гребнями (рис. 3.1, б). Например, рельеф функции Ф(х, у) = 10(y – sin x)2 + 0,1 x 2, (3.3) изображенный на этом рисунке, имеет ярко выраженный извилистый разрешимый овраг, «дно» которого – синусоида, а низшая точка – начало координат. В физических задачах овражный рельеф указывает на то, что вычислитель не учёл какую-то закономерность, имеющую вид связи между переменными. Обнаружение и явный учёт этой закономерности облегчают решение математической задачи. Так, если в примере (3.3) ввести новые переменные ξ = х, η = y – sin x, то рельеф становится котловинным. Неупорядоченный тип рельефа (рис. 3.1, в) характеризуется наличием многих максимумов, минимумов и седловин. Примером может служить функция Ф(х, у) = (1 + sin2 x)(1 + sin2 y), (3.4) рельеф которой изображён на этом рисунке; она имеет минимумы в точках с координатами Все эффективные методы поиска минимума сводятся к построению траекторий, вдоль которых функция убывает; разные методы отличаются способами построения таких траекторий. Метод, приспособленный к одному типу рельефа, может оказаться плохим на рельефе другого типа.
|

 , (3.1)
, (3.1) , (3.2)
, (3.2) ,
, 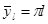 и максимумы в точках, сдвинутых относительно минимумов на π/2 по каждой координате.
и максимумы в точках, сдвинутых относительно минимумов на π/2 по каждой координате.


