Метод золотого сечения
Золотым сечением отрезка называется такое разбиение отрезка на две неравные части, что отношение длины всего отрезка к длине его большей части равно отношению длины большей части к длине меньшей части отрезка. Золотое сечение [ A, B ] осуществляется каждой из двух симметрично расположенных относительно центра отрезка точек α и β:
Можно проверить:
 
α осуществляет золотое сечение отрезков [ A, B ] и [ A, b ], β осуществляет золотое сечение отрезков [ A, B ] и [α, B ]. Очередная (k+1)-я итерация осуществляется аналогично (k+1)-ой итерации метода дихотомии. На очередном отрезке [ A (k ) ,B (k)] выберем две симметрично расположенные точки α(k) и β(k):
где D(k) = B (k) – A (k) Важно, что какой бы из отрезков [ A (k), b (k)] или [ a (k), B (k)] не был бы выбран за очередной отрезок локализации, точка x (k+1) совпадает с одной из точек a (k+1), b (k+1). Таким образом, на очередном шаге достаточно вычислить значение функции лишь в одной недостающей точке. x (n) отстоит от концов отрезка [ A (n), B (n)] на величину меньшую Соотношение Каждая итерация сокращает длину отрезка локализации в Таким образом где D = B – A - длина отрезка [ A, B ]. На рис.2.5 приведена блок-схема алгоритма процедуры GOLD(A, B, Eps, X0), выполняющей поиск абсциссы точки, в которой целевая функция F(x) достигает своего минимума методом золотого сечения. F(x) – заданная целевая функция – должна быть описана отдельно. Входные параметры: А, B – значения концов отрезка локализации [ A, B ]; Eps – заданная точность вычислений; Выходные параметры: X0 - приближение к искомому значению абсциссы точки минимума;
         FA £ FB FA £ FB
Beta = Alfa Alfa = Beta
Рисунок 2.5 - Блок-схема алгоритма процедуры GOLD
|




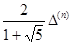
 можно использовать как оценку.
можно использовать как оценку. раз.
раз.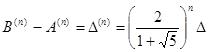
 GOLD(A, B, Eps, X0)
GOLD(A, B, Eps, X0) Alfa = A + 2*(B-A)/(3+
Alfa = A + 2*(B-A)/(3+  )
) FB = F(Beta)
FB = F(Beta)








 +
+ end
end


