Метод дробления шага
Как нетрудно понять, на каждой итерации было бы желательно выбирать направление спуска p ( n ), близкое к тому направлению, перемещение вдоль которого приводит из точки х ( n ) в точку В одном из простейших алгоритмов (типа дробления шага) такого выбора шага αn фиксируют начальное значение α; > 0 и значение параметра γ, 0 < γ < 1. За αn принимают αn =
Однако при таком выборе αn нет гарантии, что последовательность х ( n ) будет сходиться к точке минимума даже для простой квадратичной функции. Условие (3.14) является слишком слабым: последовательность х ( n ), незначительно уменьшая значения функции f, может «останавливаться», не доходя до точки
Здесь β; (0 < β; < 0) – дополнительный параметр. Пример 4. Продемонстрируем применение градиентного метода с дроблением шага к задаче минимизации квадратичной функции f(x, y) = x2 + 2y2 – 4x – 4y из примера 2. Для выбора значения шага будем использовать условие (3.15). Воспользуемся следующими краткими обозначениями: αi = α; γ i, х ( n,i ) = х ( n ) - αi g ( n ) , где g ( n ) = (2 x ( n ) – 4, 4 y ( n ) – 4)T. Выберем начальное приближение х (0) = (0, 0)Т, начальное значение шага Вычислим значения f(х (0) ) = 0, g (0) = (-4, -4)Т. 1-я итерация. Вычисляем х (0,0) = х (0) – α0 g (0) = (4, 4)Т, f(х (0,0) ) = 16. Так как значение функции не уменьшилось, то следует уменьшить шаг: α;1 = α0 /2 = 0.5. 1) Вычисляем х (0,1) = х (0) – α1 g (0) = (2, 2)Т, f(х (0,1) ) = -4. Поскольку, f(х (0,1) ) - f(х (0) ) = -4 > - β α;1| g (0)|2 = -12, условие (3.15) не выполняется и следует снова уменьшить шаг: α;2 = α;1 /2 = 0.25. 2) Вычисляем х (0,2) = х (0) – α2 g (0) = (1, 1)Т, f(х (0,2) ) = -5. Имеем f(х (0,2) ) - f(х (0) ) = -5 > - β α;2| g (0)|2 = -6, т.е. условие (3.15) не выполняется. Уменьшаем шаг: α;3 = α;2 /2 = 0.125. 3) Вычисляем х (0,3) = х (0) – α3 g (0) = (0.5, 0.5)Т, f(х (0,3) ) = -3.25. Так как f(х (0,3) ) - f(х (0) ) = -3.25 < - β α;3| g (0)|2 = -3, то условие (3.15) выполнено. 4) Положим х (1) = х (0,3) = (0.5, 0.5)Т, f(х (1) ) = -3.25. Вычислим g (1) = (-3, -2)Т и положим α0 = 1. Далее вычисления следует продолжить до выполнения какого-либо принятого критерия окончания итераций. На рис.3.9 приведена блок-схема алгоритма метода дробления шага для минимизации рассмотренной в этом примере квадратичной функции.
Начало
   FI – F0 < -B*A*M FI – F0 < -B*A*M
  T = T = 
 T < Eps T < Eps
Рисунок 3.9 - Блок-схема алгоритма метода дробления шага для функции двух переменных Входные данные: X, Y – координаты точки начального приближения из заданной области Х0 £Х £ ХN, Y0 £ Y £ YN; Eps – заданная точность вычислений; B – дополнительный параметр метода β; (в примере β; = ¾); G – параметр γ (0 < γ < 1), обеспечивающий дробление шага; F(x, y) – заданная целевая функция – должна быть описана отдельно; G1(x, y) – функция - частная производная функции F(x, y) по переменной х; G2(x, y) – функция - частная производная функции F(x, y) по переменной y; Результаты: X, Y - приближение к искомым значениям координат точки минимума; F0 = F(X,Y) – значение целевой функции в точке минимума.
|

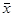 . К сожалению, антиградиент p ( n ) = - g ( n ) является, как правило, неудачным направлением спуска. Особенно ярко это проявляется для овражных функций. Поэтому возникает сомнение в целесообразности тщательного поиска решения задачи одномерной минимизации (3.13) и появляется желание сделать в направлении p ( n ) лишь такой шаг, который бы обеспечил «существенное убывание» функции f. Более того, на практике иногда довольствуются определением значения
. К сожалению, антиградиент p ( n ) = - g ( n ) является, как правило, неудачным направлением спуска. Особенно ярко это проявляется для овражных функций. Поэтому возникает сомнение в целесообразности тщательного поиска решения задачи одномерной минимизации (3.13) и появляется желание сделать в направлении p ( n ) лишь такой шаг, который бы обеспечил «существенное убывание» функции f. Более того, на практике иногда довольствуются определением значения  , где in – первый из номеров i = 0, 1, 2, …, для которого выполнено условие убывания
, где in – первый из номеров i = 0, 1, 2, …, для которого выполнено условие убывания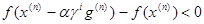 . (3.14)
. (3.14)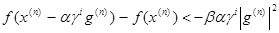 . (3.15)
. (3.15)

 Ввод Х, Y, Eps, B, G
Ввод Х, Y, Eps, B, G


 F0 = F(X, Y)
F0 = F(X, Y)
 A = 2
A = 2

 F2 = G2(X, Y)
F2 = G2(X, Y)
 M = F12 + F22
M = F12 + F22


 A = A * G
A = A * G



 Вывод (X, Y), F0
Вывод (X, Y), F0
 end
end


