Методы прямого поиска. Оптимальный пассивный поиск
Ряд методов минимизации основан на сравнении значений функции f, вычисляемых в точках х 1, х 2, …, хN. Эти методы часто называют методами прямого поиска, а точки хi - пробными точками. Уточним постановку задачи. Требуется найти приближение Оптимальный пассивный поиск. Метод решения поставленной задачи, в котором задаётся правило вычисления сразу всех пробных точек х 1, х 2, …, хN и за Оценим погрешность этого метода. Для удобства положим х 0 = A, хN+1 = B. В силу выбора точки | Так как положение точки минимума
Можно показать, что величина, стоящая в правой части неравенства (1), станет минимальной, если точки х 1, х 2, …, хN расположить на отрезке [ A, B ] равномерно в соответствии с формулой xi = A + ih, где h =
Пример 2. Используем оптимальный пассивный поиск для того, чтобы найти с точностью ε = 0.1 точку Из формулы (2) следует, что для решения задачи потребуется вычислить значения функции в девяти пробных точках вида xi = 0.1 i, где i = 1, 2, …, 9. Приведём таблицу этих значений:
Так как минимальное значение достигается в точке х 7 = 0.7, то Если бы мы попытались найти На рис 2.1 приведена блок-схема алгоритма метода оптимального пассивного поиска. F(x) – заданная целевая функция – должна быть описана отдельно. Входные данные: А, B – значения концов отрезка локализации [ A, B ]; Eps – заданная точность вычислений; Результаты: Xmin - приближение к искомому значению абсциссы точки минимума; Fmin – значение целевой функции в точке минимума.
Начало
 Fmin > Fx Fmin > Fx
Рисунок 2.1 - Блок-схема алгоритма метода оптимального пассивного поиска
|

 к точке минимума
к точке минимума  унимодальной на отрезке [ A, B ] функции f. Предположим также, что число пробных точек N заранее фиксируется и за приближение
унимодальной на отрезке [ A, B ] функции f. Предположим также, что число пробных точек N заранее фиксируется и за приближение  , называется методом пассивного поиска.
, называется методом пассивного поиска. справедливы неравенства f (xk-1) ≥ f (xk) и f (xk) ≤ f (xk+1). Поэтому из п.3 утверждения 2 следует, что
справедливы неравенства f (xk-1) ≥ f (xk) и f (xk) ≤ f (xk+1). Поэтому из п.3 утверждения 2 следует, что  [ xk-1, xk+1 ]. Следовательно,
[ xk-1, xk+1 ]. Следовательно, на отрезке [ A, B ] заранее неизвестно, то для
на отрезке [ A, B ] заранее неизвестно, то для  справедлива лишь следующая гарантированная оценка погрешности:
справедлива лишь следующая гарантированная оценка погрешности: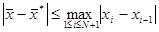 . (2.1)
. (2.1) , Δ = B – A. Метод с таким выбором пробных точек называется оптимальным пассивным поиском. Гарантированная оценка погрешности для него выглядит так:
, Δ = B – A. Метод с таким выбором пробных точек называется оптимальным пассивным поиском. Гарантированная оценка погрешности для него выглядит так: . (2.2)
. (2.2)

 Ввод А, В, Eps
Ввод А, В, Eps
 N = round ((B - A)/Eps)
N = round ((B - A)/Eps)
 i = 1.. N
i = 1.. N
 x = A + i* Eps
x = A + i* Eps



 Xmin = x
Xmin = x


 Вывод Xmin, Fmin
Вывод Xmin, Fmin end
end


