Глобальный оптимум
Глобальный оптимум – это оптимальное решение для всего пространства проектирования. Оно лучше всех других решений, соответствующих локальным оптимумам, и именно его ищет конструктор. Покажем на примере, как ставится задача оптимизации. Пример 1.
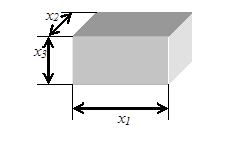 Пусть требуется спроектировать контейнер объёмом 1 м3, предназначенный для перевозки неупакованного волокна (рис.1.2). Желательно, чтобы на изготовление таких контейнеров затрачивалось как можно меньше материала (при условии постоянства толщины стенок это означает, что площадь поверхности должна быть минимальной), так как при этом он будет дешевле. Чтобы контейнер удобно было брать автопогрузчиком, его ширина должна быть не менее 1,5 м. Пусть требуется спроектировать контейнер объёмом 1 м3, предназначенный для перевозки неупакованного волокна (рис.1.2). Желательно, чтобы на изготовление таких контейнеров затрачивалось как можно меньше материала (при условии постоянства толщины стенок это означает, что площадь поверхности должна быть минимальной), так как при этом он будет дешевле. Чтобы контейнер удобно было брать автопогрузчиком, его ширина должна быть не менее 1,5 м.
Сформулируем эту задачу в виде, удобном для применения алгоритма оптимизации. Проектные параметры: x1, x2, x3. Целевая функция (которую требуется минимизировать) – площадь боковой поверхности контейнера: F = 2(x1x2 + x2x3 + x1x3), м2. Ограничение – равенство: Объём = x1x2x3 = 1 м3. Ограничение – неравенство: x1 ³ 1,5 м. Внимательный конструктор заметит, что ограничение – равенство благодаря своей простоте позволяет уменьшить размерность задачи. Действительно, если x3 = 1/ x1x2, то x3 можно исключить из проектных параметров. Формулируя вновь задачу, имеем: Проектные параметры: x1, x2. Целевая функция: F = 2(x1x2 + Ограничение – равенство: нет. Ограничение – неравенство: x1 ³ 1,5 м. После того, как задача сформулирована стандартным способом, её можно решать любым методом. Если воспользоваться обычным определением минимума и принять то будет получен результат: x1 = x2 = x3 = 1 м. Однако, при таком решении не удовлетворено ограничение – неравенство и, следовательно, оно неприемлемо. Этот пример служит иллюстрацией важного обстоятельства, связанного с оптимизацией и состоящего в том, что в связи с введением дополнительных условий оптимальное решение может соответствовать точке, в которой локальный градиент не равен нулю. Чтобы полностью решить эту задачу, придётся воспользоваться методами, изложенными далее.
|

 +
+  ), м2.
), м2.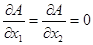 ,
,


