Эпидемиология и профилактика
Таблица 1.
Значения функции 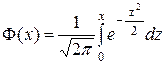
| х
| Ф(х)
| х
| Ф(х)
| х
| Ф(х)
| х
| Ф (х)
| | 0,00
| 0,0000
| 0,31
| 0,1217
| 0,62
| 0,2324
| 0,93
| 0,3238
| | 0,01
| 0,0040
| 0,32
| 0,1255
| 0,63
| 0,2357
| 0,94
| 0,3264
| | 0,02
| 0,0080
| 0,33
| 0,1293
| 0,64
| 0,2389
| 0,95
| 0,3289
| | 0,03
| 0,0120
| 0,34
| 0,1331
| 0,65
| 0,2422
| 0,96
| 0,3315
| | 0,04
| 0,0160
| 0,35
| 0,1368
| 0,66
| 0,2454
| 0,97
| 0,3340
| | 0,05
| 0,0199
| 0,36
| 0,1406
| 0,67
| 0,2486
| 0,98
| 0,3365
| | 0,06
| 0,0239
| 0,37
| 0,1443
| 0,68
| 0,2517
| 0,99
| 0,3389
| | 0,07
| 0,0279
| 0,38
| 0,1480
| 0,69
| 0,2549
| 1,00
| 0,3413
| | 0,08
| 0,0319
| 0,39
| 0,1517
| 0,70
| 0,2580
| 1,01
| 0,3438
| | 0,09
| 0,0359
| 0,40
| 0,1554
| 0,71
| 0,2611
| 1,02
| 0,3461
| | 0,10
| 0,0398
| 0,41
| 0,1591
| 0,72
| 0,2642
| 1,03
| 0,3485
| | 0,11
| 0,0438
| 0,42
| 0,1628
| 0,73
| 0,2673
| 1,04
| 0,3508
| | 0,12
| 0,0478
| 0,43
| 0,1664
| 0,74
| 0,2703
| 1,05
| 0,3531
| | 0,13
| 0,0517
| 0,44
| 0,1700
| 0,75
| 0,2734
| 1,06
| 0,3554
| | 0,14
| 0,0557
| 0,45
| 0,1736
| 0,76
| 0,2764
| 1,07
| 0,3577
| | 0,15
| 0,0596
| 0,46
| 0,1772
| 0,77
| 0,2794
| 1,08
| 0,3599
| | 0,16
| 0,0636
| 0,47
| 0,1808
| 0,78
| 0,2823
| 1,09
| 0,3621
| | 0,17
| 0,0675
| 0,48
| 0,1844
| 0,79
| 0,2852
| 1,10
| 0,3643
| | 0,18
| 0,0714
| 0,49
| 0,1879
| 0,80
| 0,2881
| 1,11
| 0,3665
| | 0,19
| 0,0753
| 0,50
| 0,1915
| 0,81
| 0,2910
| 1,12
| 0,3686
| | 0,20
| 0,0793
| 0,51
| 0,1950
| 0,82
| 0,2939
| 1,13
| 0,3708
| | 0,21
| 0,0832
| 0,52
| 0,1985
| 0,83
| 0,2967
| 1,14
| 0,3729
| | 0,22
| 0,0871
| 0,53
| 0,2019
| 0,84
| 0,2995
| 1,15
| 0,3749
| | 0,23
| 0,0910
| 0,54
| 0,2054
| 0,85
| 0,3023
| 1,16
| 0,3770
| | 0,24
| 0,0948
| 0,55
| 0,2088
| 0,86
| 0,3051
| 1,17
| 0,3790
| | 0,25
| 0,0987
| 0,56
| 0,2123
| 0,87
| 0,3078
| 1,18
| 0,3810
| | 0,26
| 0,1026
| 0,57
| 0,2157
| 0,88
| 0,3106
| 1,19
| 0,3830
| | 0,27
| 0,1064
| 0,58
| 0,2190
| 0,89
| 0,3133
| 1,20
| 0,3849
| | 0,28
| 0,1103
| 0,59
| 0,2224
| 0,90
| 0,3159
| 1,21
| 0,3869
| | 0,29
| 0,1141
| 0,60
| 0,2257
| 0,91
| 0,3186
| 1,22
| 0,3883
| | 0,30
| 0,1179
| 0,61
| 0,2291
| 0,92
| 0,3212
| 1,23
| 0,3907
| | | | | | | | | | |
Продолжение таблицы 1.
| х
| Ф(х)
| х
| Ф(х)
| х
| Ф(х)
| х
| Ф (х)
| | 1,24
| 0,3925
| 1,58
| 0,4429
| 1,92
| 0,4726
| 2,52
| 0,4941
| | 1,25
| 0,3944
| 1,59
| 0,4441
| 1,93
| 0,4732
| 2,54
| 0,4945
| | 1,26
| 0,3962
| 1,60
| 0,4452
| 1,94
| 0,4738
| 2,56
| 0,4948
| | 1,27
| 0,3980
| 1,61
| 0,4463
| 1,95
| 0,4744
| 2,58
| 0,4951
| | 1,28
| 0,3997
| 1,62
| 0,4474
| 1,96
| 0,4750
| 2,60
| 0,4953
| | 1,29
| 0,4015
| 1,63
| 0,4484
| 1,97
| 0,4756
| 2,62
| 0,4956
| | 1,30
| 0,4032
| 1,64
| 0,4495
| 1,98
| 0,4761
| 2,64
| 0,4959
| | 1,31
| 0,4049
| 1,65
| 0,4505
| 1,99
| 0,4767
| 2,66
| 0,4961
| | 1,32
| 0,4066
| 1,66
| 0,4515
| 2,00
| 0,4772
| 2,68
| 0,4963
| | 1,33
| 0,4082
| 1,67
| 0,4525
| 2,02
| 0,4783
| 2,70
| 0,4965
| | 1,34
| 0,4099
| 1,68
| 0,4535
| 2,04
| 0,4793
| 2,72
| 0,4967
| | 1,35
| 0,4115
| 1,69
| 0,4545
| 2,06
| 0,4803
| 2,74
| 0,4969
| | 1,36
| 0,4131
| 1,70
| 0,4554
| 2,08
| 0,4812
| 2,76
| 0,4971
| | 1,37
| 0,4147
| 1,71
| 0,4564
| 2,10
| 0,4821
| 2,78
| 0,4973
| | 1,38
| 0,4162
| 1,72
| 0,4573
| 2,12
| 0,4830
| 2,80
| 0,4974
| | 1,39
| 0,4177
| 1,73
| 0,4582
| 2,14
| 0,4838
| 2,82
| 0,4976
| | 1,40
| 0,4192
| 1,74
| 0,4591
| 2,16
| 0,4846
| 2,84
| 0,4977
| | 1,41
| 0,4207
| 1,75
| 0,4599
| 2,18
| 0,4854
| 2,86
| 0,4979
| | 1,42
| 0,4222
| 1,76
| 0,4608
| 2,20
| 0,4861
| 2,88
| 0,4980
| | 1,43
| 0,4236
| 1,77
| 0,4616
| 2,22
| 0,4868
| 2,90
| 0,4981
| | 1,44
| 0,4251
| 1,78
| 0,4625
| 2,24
| 0,4875
| 2,92
| 0,4982
| | 1,45
| 0,4265
| 1,79
| 0,4633
| 2,26
| 0,4881
| 2,94
| 0,4984
| | 1,46
| 0,4279
| 1,80
| 0,4641
| 2,28
| 0,4887
| 2,96
| 0,4985
| | 1,47
| 0,4292
| 1,81
| 0,4649
| 2,30
| 0,4893
| 2,98
| 0,4986
| | 1,48
| 0,4306
| 1,82
| 0,4656
| 2,32
| 0,4898
| 3,00
| 0,49865
| | 1,49
| 0,4319
| 1,83
| 0,4664
| 2,34
| 0,4904
| 3,20
| 0,49931
| | 1,50
| 0,4332
| 1,84
| 0,4671
| 2,36
| 0,4909
| 3,40
| 0,49966
| | 1,51
| 0,4345
| 1,85
| 0,4678
| 2,38
| 0,4913
| 3,60
| 0,499841
| | 1,52
| 0,4357
| 1,86
| 0,4686
| 2,40
| 0,4918
| 3,80
| 0,499928
| | 1,53
| 0,4370
| 1,87
| 0,4693
| 2,42
| 0,4922
| 4,00
| 0,499968
| | 1,54
| 0 4382
| 1,88
| 0,4690
| 2,44
| 0,4927
| 4,50
| 0,499997
| | 1,55
| 0,4394
| 1,89
| 0,4706
| 2,46
| 0,4931
| 5,00
| 0,49999997
| | 1,56
| 0,4406
| 1,90
| 0,4713
| 2,48
| 0,4934
| ¥
| 0,5
| | 1,57
| 0,4418
| 1,91
| 0,4719
| 2,50
| 0,4938
|
|
| | | | | | | | | | |
Таблица 2.
Распределение Пуассона 
т – число появлений события в п независимых испытаниях,
а = тр – среднее число появлений события в п испытаниях.
 а
т а
т
| 0,1
| 0,2
| 0,3
| 0,4
| 0,5
| 0,6
| 0,7
| 0,8
| 0,9
| 1,0
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
| —
| —
| —
|
|
|
|
|
|
|
| |
| —
| —
| —
| —
| —
| —
|
|
|
|
| |
| —
| —
| —
| —
| —
| —
| —
| —
| —
|
|
 а
т а
т
| 1,1
| 1,2
| 1,3
| 1, 4
| 1,5
| 1,6
| 1,7
| 1,8
| 1,9
| 2,0
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
| —
| —
|
|
|
|
|
|
|
|
| |
| —
| —
| —
| —
| —
| —
|
|
|
|
|
 а
т а
т
| 2,1
| 2,2
| 2,3
| 2,4
| 2,5
| 2,6
| 2,7
| 2,8
| 2,9
| 3,0
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
Продолжение табл.2.
 а
т а
т
| 3,5
| 4,0
| 4,5
| 5,0
| 6,0
| 7,0
| 8,0
| 9,0
| 10,0
| 11,0
| |
|
—
—
—
—
—
—
—
—
—
—
—
—
—
|
—
—
—
—
—
—
—
—
—
—
—
—
|
—
—
—
—
—
—
—
—
—
—
—
|
—
—
—
—
—
—
—
—
—
—
—
|
—
—
—
—
—
—
—
—
—
|
—
—
—
—
—
—
—
|
—
—
—
—
—
|
—
—
—
—
| -
—
—
| -
—
|
Примечание. В таблице даны значения вероятности  после запятой. после запятой.
Таблица 3.
Критические точки распределения Стьюдента.
В таблице приведены значения  в зависимости от объема выборки п (числа степеней свободы k = п – 1) и надежности g (уровня значимости a =1 - g), для которых выполняется условие в зависимости от объема выборки п (числа степеней свободы k = п – 1) и надежности g (уровня значимости a =1 - g), для которых выполняется условие  (вероятность того, что случайная величина t по абсолютной величине меньше критического значения (вероятность того, что случайная величина t по абсолютной величине меньше критического значения  равна доверительной вероятности g). равна доверительной вероятности g).
| Надежность g
| 0,9
| 0,95
| 0,99
| 0,995
| 0,999
| | Уровень значимости a
| 0,1
| 0,05
| 0,01
| 0,005
| 0,001
| | Объем выборки
п
| Число степеней свободы k
| | | | | | |
|
| 6,314
2,920
2,353
2,132
2,015
1,943
1,895
1,860
1,833
1,813
1,796
1,782
1,771
1,761
1,753
1,746
1,740
1,734
1,729
1,725
1,721
1,717
1,714
1,711
1,708
1,706
1,703
1,701
1,699
| 12,706
4,303
3,183
2,776
2,571
2,447
2,365
2,306
2,262
2,228
2,201
2,179
2,160
2,145
2,131
2,120
2,110
2,101
2,093
2,086
2,080
2,074
2,069
2,064
2,060
2,055
2,052
2,048
2,045
| 63,657
9,925
5,841
4,604
4,032
3,707
3,500
3,355
3,250
3,169
3,106
3,054
3,012
2,977
2,947
2,921
2,898
2,878
2,861
2,845
2,831
2,819
2,807
2.797
2,787
2,779
2,771
2,763
2,756
| 127,32
14,089
7,453
5,597
4,773
4,317
4,029
3,833
3,690
3,581
3,497
3,428
3,372
3,326
3,286
3,252
3,222
3,193
3,174
3,153
3,135
3,119
3,104
3,092
3,078
3,067
3,056
3,047
3,038
| 636,62
31,600
12,922
8,610
6,869
5,959
5,408
5,041
4,781
4,587
4,437
4,318
4,221
4,140
4,073
4,015
3,965
3,922
3,883
3,849
3,819
3,792
3,767
3,745
3,725
3,707
3,690
3,674
3,659
|
Таблица 4.
Критические точки распределения  . .
(для малых значений уровня значимости a).
В таблице приведены критические значения 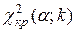 , для которых выполняется условие , для которых выполняется условие
 (вероятность того, что случайная величина (вероятность того, что случайная величина  превысит значение превысит значение  равна уровню значимости a). равна уровню значимости a).
| Число степеней свободы k
| Уровень значимости a
| | 0,2
| 0,1
| 0,05
| 0,025
| 0,01
| 0,005
| 0,001
| 0,0005
| |
|
1,64
3,22
4,64
5,99
7,29
8,56
9,80
11,03
12,24
13,44
14,63
15,81
16,98
18,15
19,31
20,46
21,61
22,76
23,90
25,04
26,17
27,30
28,43
29,55
30,67
31,79
32,91
34,03
35,14
36,25
| 2,71
4,61
6,25
7,78
9,24
10,64
12,02
13,36
14,68
15,99
17,27
18,55
19,81
21,06
22,31
23,54
24,77
25,99
27,20
28,41
29,61
30,81
32,01
33,20
34,38
35,56
36,74
37,92
39,09
40,26
| 3,84
5,99
7,81
9,49
11,07
12,59
14,07
15,51
16,92
18,31
19,67
21,03
22,36
23,68
25,00
26,30
27,59
28,87
30,14
31,41
32,67
33,92
35,17
36,41
37,65
38,88
40,11
41,34
42,56
43,77
| 5,02
7,38
9,35
11,14
12,83
14,45
16,01
17,53
19,02
20,48
21,92
33,34
24,74
26,12
27,49
28,84
30,19
31,53
32,85
34,17
35,48
36,78
38,08
39,36
40,65
41,92
43,19
44,46
45,72
46,98
| 6,63
9,21
11,34
13,28
15,09
16,81
18,47
20,09
21,67
23,21
24,72
26,22
27,69
29,14
30,58
32,00
33,41
34,80
36,19
37,57
38,93
40,29
41,64
42,98
44,31
45,64
46,96
48,28
49,59
50,89
| 7,88
10,60
12,84
14,86
16,75
18,55
20,28
21,95
23,59
25,19
26,76
28,30
29,82
31,32
32,80
34,27
35,72
37,16
38,58
40,00
41,40
42,80
44,18
45,56
46,93
48,29
49,64
50,99
52,34
53,67
| 10,83
13,82
16,27
18,47
20,51
22,46
24,32
26,12
27,88
29,59
31,26
32,91
34,53
36,12
37,70
39,25
40,80
42,31
43,82
45,31
46,80
48,27
49,73
51,18
52,62
54,05
55,48
56,89
58,30
59,70
| 12,12
15,20
17,73
20,00
22,10
24,10
26,02
27,87
29,67
31,42
33,14
34,82
36,48
38,11
39,72
41,31
42,88
44,43
45,97
47,50
49,01
50,51
52,00
53,48
54,95
56,41
57,86
59,30
60,73
62,16
|
Примерный список рекомендуемой литературы
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. - М.: Наука, 1984.
2. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисления.-М.:Наука, 1988.
3. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. -М.: Наука, 1967.
4. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. -М.: Наука, 1984.
5. Булдык Г.М. Теория вероятностей и математическая статистика. -Минск, Высшая школа, 1989.
6. Вентцель Е.С. Теория вероятностей, Физматгиз, 1962.
7. Воеводин В.В. Численные методы алгебры.
8. Воробьев Н.Н. Теория рядов.
9. Высшая математика: Методические указания для самостоятельной работы студентов заочного факультета РСХИ /сост. Т.С. Белоусова, Н.И. Потлова, В.И. Сусойкин, Е.И. Троицкий, О.В. Балашова, С.Н. Панкрашкина /- Рязань: РСХИ, 1989. Часть I.
10.Высшая математика: Методические указания для самостоятельной работы студентов заочного факультета РСХИ /сост. Е.И. Троицкий, Т.С. Белоусова, С.Н. Панкрашкина/ - Рязань: РСХИ, 1992, часть II.
11.Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике.
10.Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 1972.
11.Данко П.В., Попов А.Г., Кожевникова Т.Н. Высшая математика в упражнениях и задачах: в2ч. - М.: Высшая школа, 1986.
12. Давыдочкина С.В.. Основные понятия операционного исчисления и его приложения. /Для студентов технических специальностей сельскохозяйственных вузов. Рязань, РГСХА, 2004 г.
13.Давыдочкина С.В. Векторная алгебра. – РГСХА, 2002 г., 43 с.
14.Доспехов Б.А. Методика полевого опыта (с основами статистической отработки результатов исследований) - М.: Агропромиздат, 1985.
13.Ефимов А.В., Золотарев А.В., Терпигорева В.М. Математический анализ (специальные разделы), часть II. М.: Высшая школа, 1980.
14.Ефимов Н.В. Краткий курс аналитической геометрии. - М.: Наука, 1975.
15.3айцев И.А. Высшая математика. - Высшая школа, 1991.
16.Кальницкий Л.А., Добротин О.А., Жевержеев В.Ф. Специальный курс высшей математики, «Высшая школа», 1976.
17.Квальвассер В.И., Фридман М.И. Теория поля. Теория функций комплексного переменного. Операционное исчисление. М.: Высшая школа, 1967.
18.Краснов М.Л., Киселев А.И., Макаренко Г.И. Векторный анализ. - М.: Наука, 1978.
19.Лачуга Ю.Ф., Самсонов В.А., Дидманидзе О.Н. Прикладная математика. Нелинейное программирование в инженерных задачах. — М.: Колос, 2001.
20.Матвеев Н.М. 'Методы интегрирования обыкновенных дифференциальных уравнений. -М.: Высшая школа, 1967.
21.Минорский В.П. Сборник задач по высшей математике. - М.: Наука, 1977.
22.Пискунов Н.С. Дифференциальное и интегральное исчисления. - М.: Наука, 1978, т. 1,2.
23.Поллард Дж. Справочник по вычислительным методам статистики / Пер. с англ.-М.: Финансы и статистика, 1982.
24.Пономарев К.К. Специальный курс высшей математики.
25.Романовский П.И. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа. - М.: Наука, 1973.
26.Фихтенгольц Г.М. Основы математического анализа.
27.Шипачев В.С. Высшая математика. М. «Высшая школа», 1985.
Эпидемиология и профилактика

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|
Субъективные признаки контрабанды огнестрельного оружия или его основных частей
Переходя к рассмотрению субъективной стороны контрабанды, остановимся на теоретическом понятии субъективной стороны состава преступления...
ЛЕЧЕБНО-ПРОФИЛАКТИЧЕСКОЙ ПОМОЩИ НАСЕЛЕНИЮ В УСЛОВИЯХ ОМС 001. Основными путями развития поликлинической помощи взрослому населению в новых экономических условиях являются все...
МЕТОДИКА ИЗУЧЕНИЯ МОРФЕМНОГО СОСТАВА СЛОВА В НАЧАЛЬНЫХ КЛАССАХ В практике речевого общения широко известен следующий факт: как взрослые...
|
Приложение Г: Особенности заполнение справки формы ву-45
После выполнения полного опробования тормозов, а так же после сокращенного, если предварительно на станции было произведено полное опробование тормозов состава от стационарной установки с автоматической регистрацией параметров или без...
Измерение следующих дефектов: ползун, выщербина, неравномерный прокат, равномерный прокат, кольцевая выработка, откол обода колеса, тонкий гребень, протёртость средней части оси
Величину проката определяют с помощью вертикального движка 2 сухаря 3 шаблона 1 по кругу катания...
Неисправности автосцепки, с которыми запрещается постановка вагонов в поезд. Причины саморасцепов ЗАПРЕЩАЕТСЯ: постановка в поезда и следование в них вагонов, у которых автосцепное устройство имеет хотя бы одну из следующих неисправностей:
- трещину в корпусе автосцепки, излом деталей механизма...
|
|

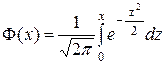

 а
т
а
т
 после запятой.
после запятой. в зависимости от объема выборки п (числа степеней свободы k = п – 1) и надежности g (уровня значимости a =1 - g), для которых выполняется условие
в зависимости от объема выборки п (числа степеней свободы k = п – 1) и надежности g (уровня значимости a =1 - g), для которых выполняется условие  (вероятность того, что случайная величина t по абсолютной величине меньше критического значения
(вероятность того, что случайная величина t по абсолютной величине меньше критического значения  равна доверительной вероятности g).
равна доверительной вероятности g). .
.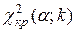 , для которых выполняется условие
, для которых выполняется условие (вероятность того, что случайная величина
(вероятность того, что случайная величина  равна уровню значимости a).
равна уровню значимости a).


