Физические приложения криволинейного интеграла первого рода.
1) Масса материальной линии. Пусть материальная (например, пространственная) кривая Г имеет в каждой своей точке
Точно такая же формула для полного заряда Q, расположенного на материальной (например, плоской) кривой Г, если известна линейная плотность зарядов в каждой точке
2) Координаты центра масс. Пусть материальная (например, пространственная) кривая Г имеет в каждой своей точке
где
Аналогично находятся координаты центра масс плоской линии. 3) Определение. Центроидом кривой Г (нематериальной, просто геометрической фигуры) называется центр масс этой кривой с любой постоянной полностью (например, равной единице). Например, если кривая Г расположена в плоскости XOY, то её центроид
где 4) Первая формула Гульдина. Площадь поверхности, полученная вращением вокруг оси кривой, расположенной в плоскости оси вращения по одну сторону от неё, равна произведению длины этой кривой окружности, которую описывает при вращении центроид этой кривой, т.е.
где L - длина кривой, 5) Момент инерции. Пусть материальная (например, пространственная) кривая Г имеет в каждой своей точке
где 6) Ньютонов (гравитационный или электрический) потенциал материальной кривой Г в данной точке
где
|

 линейную плотность массы
линейную плотность массы  Тогда масса кривой Г равна:
Тогда масса кривой Г равна:


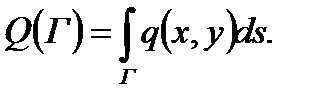
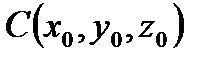 имеет координаты:
имеет координаты:
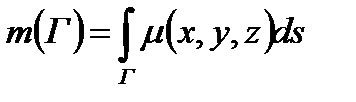 - масса этой кривой, и
- масса этой кривой, и
 имеет координаты:
имеет координаты:
 и
и  - длина кривой Г.
- длина кривой Г.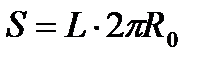
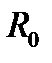 - расстояние от центроида кривой до оси вращения.
- расстояние от центроида кривой до оси вращения.
 расстояние от точки
расстояние от точки 
 расположенной вне этой кривой Г, имеющей линейную плотность (массы или соответственно заряда)
расположенной вне этой кривой Г, имеющей линейную плотность (массы или соответственно заряда) 

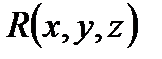 - расстояние от произвольной точки
- расстояние от произвольной точки  , т.е.
, т.е. 



