Определение криволинейного интеграла второго рода.
В этом разделе мы познакомимся с еще одним типом криволинейных интегралов. Начнем с определения ориентированной кривой в пространстве. Определение 1. Кривую Г, определяемую уравнением
будем называть ориентированной кривой, если на ней задан порядок следования точек, а именно, точка
ПРИМЕР 1. Для окружности
Эта кривая – ориентированная: при возрастании параметра отвечающего точке A происходит движение соответствующей точки кривой против часовой стрелки до точки B (для которой
Рис. 8. К примеру 1.
При построении разбиения Т в этом параграфе будем предполагать, что точки разбиения Составим три интегральные суммы: a) б) в) (1) Теперь можно дать определение криволинейного интеграла второго рода.
Определение 2. Пусть существуют пределы интегральных сумм (1) при бесконечном увеличении числа точек деления и бесконечном уменьшении длин векторов а) б) в) (2)
Тогда криволинейным интегралом второго рода, или криволинейный интеграл от векторной функции
(3) (В левой части равенства (3) под интегралом стоит скалярное произведение вектора
Определение 3. Если кривая Г замкнута, то криволинейный интеграл, определяемый формулой (3), называется циркуляцией вектора
Как и в случае криволинейных интегралов первого рода, верна теорема:
Теорема 1. Если Г – кусочно-гладкая кривая и вектор
Теорема 2. Если кривая Г задается векторным уравнением (1)п. 1.1, то интеграл (3) вычисляется по формуле:
Аналогичные формулы справедливы для каждого из интегралов (2).
Замечание. Криволинейный интеграл второго рода, в отличие от криволинейного интеграла первого рода, зависит от ориентации кривой.
При изменении ориентации (заданного направления движения по кривой) интегралы (2) – (4) меняют знак. Это связано с тем, что в определении криволинейного интеграла второго рода в интегральных суммах (1) значения координат Δ xk, Δ yk,Δ zk меняютзнак при изменении направления векторов
ПРИМЕР 2. Найти циркуляцию вектора
Рис. 9. К примеру 2.
Заметим сначала, что для точек, лежащих на контуре Г справедливы соотношения: Если начать движение по кривой Г от точки A (2, 0, – 1) в которой значение параметра
ПРИМЕР 3. Найти модуль циркуляции вектора
Рис. 10. К примеру 3.
Для точек
Поскольку в примере требуется найти модуль циркуляции, то направление обхода кривой не имеет значения (при его изменении на противоположный меняется знак всего криволинейного интеграла второго рода, а значит и циркуляции). Примем, что движение по кривой происходит в сторону увеличения параметра
откуда модуль циркуляции равен
Замечание. Все определения и утверждения, сформулированные выше для пространственных кривых, справедливы и в случае плоских кривых. В соответствующих формулах нужно лишь убрать третью координату
|

 ,
, 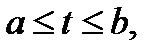
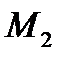 следует за точкой
следует за точкой 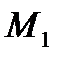 , если радиус-вектор
, если радиус-вектор 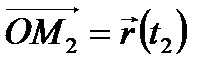 точки
точки 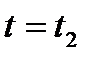 большему, чем значение параметра
большему, чем значение параметра 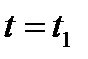 радиус-вектора
радиус-вектора 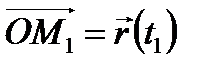 точки
точки 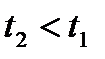 .Точка А с радиус-вектором
.Точка А с радиус-вектором  называется началом кривой, а точка В с радиус-вектором
называется началом кривой, а точка В с радиус-вектором 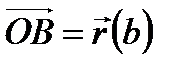 – концом кривой (см. рис.1).
– концом кривой (см. рис.1).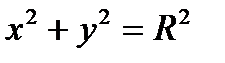 на плоскости OXY (см. рис. 8) радиус-векторы точек в параметрическом виде можно определить выражением:
на плоскости OXY (см. рис. 8) радиус-векторы точек в параметрическом виде можно определить выражением: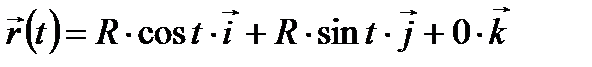 ,
,  .
.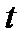 от значения
от значения 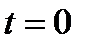 ,
,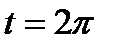 ).
).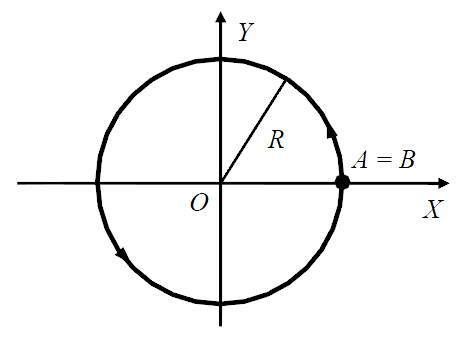
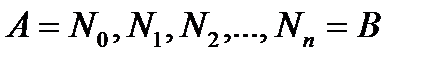 следуют друг за другом. Обозначим через
следуют друг за другом. Обозначим через 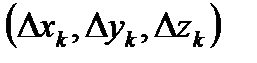 координаты вектора
координаты вектора 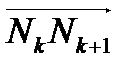 .Пусть на кривой определены три непрерывные функции:
.Пусть на кривой определены три непрерывные функции:  ,
, 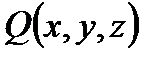 и
и 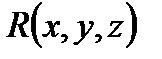 . Тогда можно считать, что на кривой Г задана вектор-функция
. Тогда можно считать, что на кривой Г задана вектор-функция 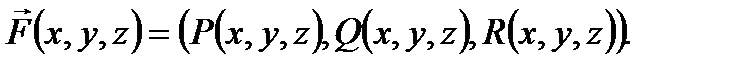
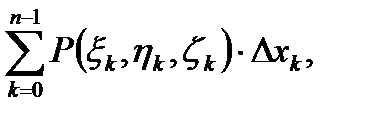
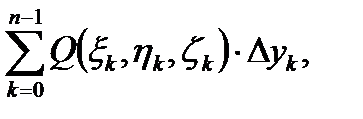
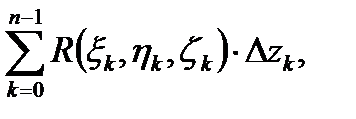
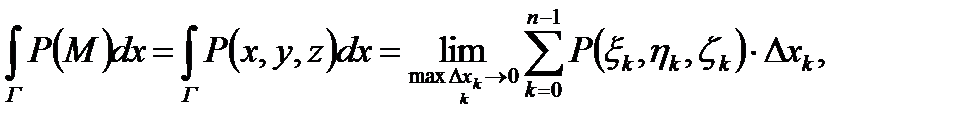
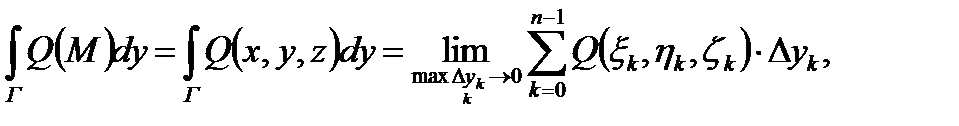
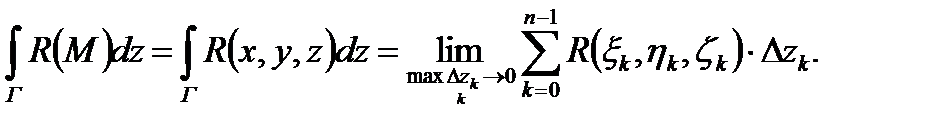
 вдоль ориентированной кривой Г, называется сумма интегралов, определенных формулой (2):
вдоль ориентированной кривой Г, называется сумма интегралов, определенных формулой (2):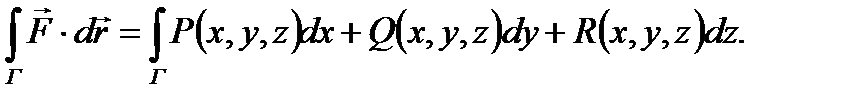
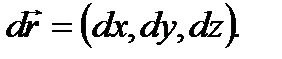
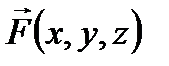 по контуру Г. Для циркуляции обычно используется обозначение
по контуру Г. Для циркуляции обычно используется обозначение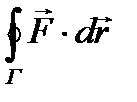
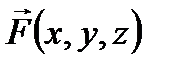 имеет непрерывные на Г компоненты
имеет непрерывные на Г компоненты 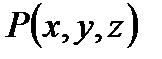 ,
, 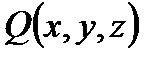 и
и 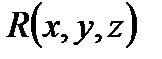 , то криволинейные интегралы (2) и (3) существуют и определены однозначно. Используя формулу для дифференцирования сложной функции получаем еще одно утверждение:
, то криволинейные интегралы (2) и (3) существуют и определены однозначно. Используя формулу для дифференцирования сложной функции получаем еще одно утверждение: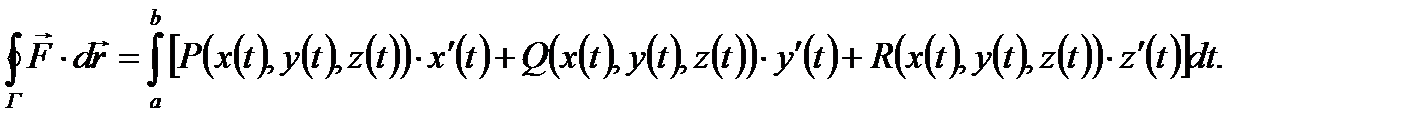
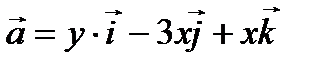 вдоль контура
вдоль контура 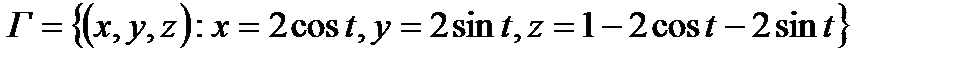 в направлении возрастания параметра t (см. рис. 9).
в направлении возрастания параметра t (см. рис. 9).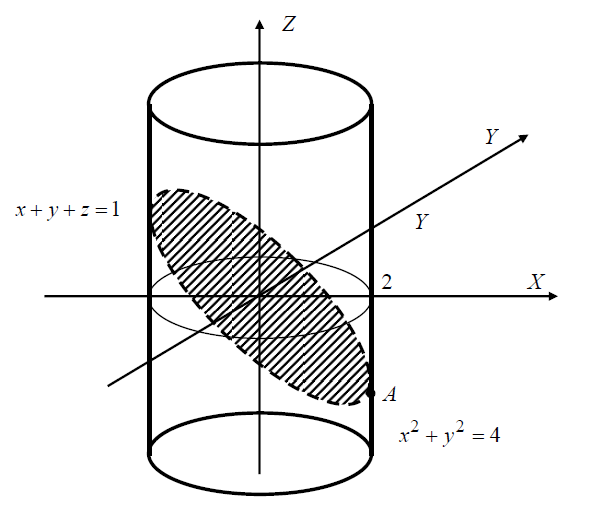
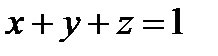 и
и 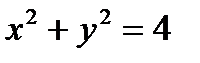 , т.е. кривая Г есть замкнутая линия пересечения цилиндра
, т.е. кривая Г есть замкнутая линия пересечения цилиндра 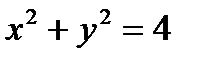 с плоскостью
с плоскостью 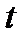 равно 0, то при изменении параметра
равно 0, то при изменении параметра 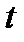 до значения 2π, точка кривой вернется в исходную точку A. Используя теорему 2, можно записать:
до значения 2π, точка кривой вернется в исходную точку A. Используя теорему 2, можно записать: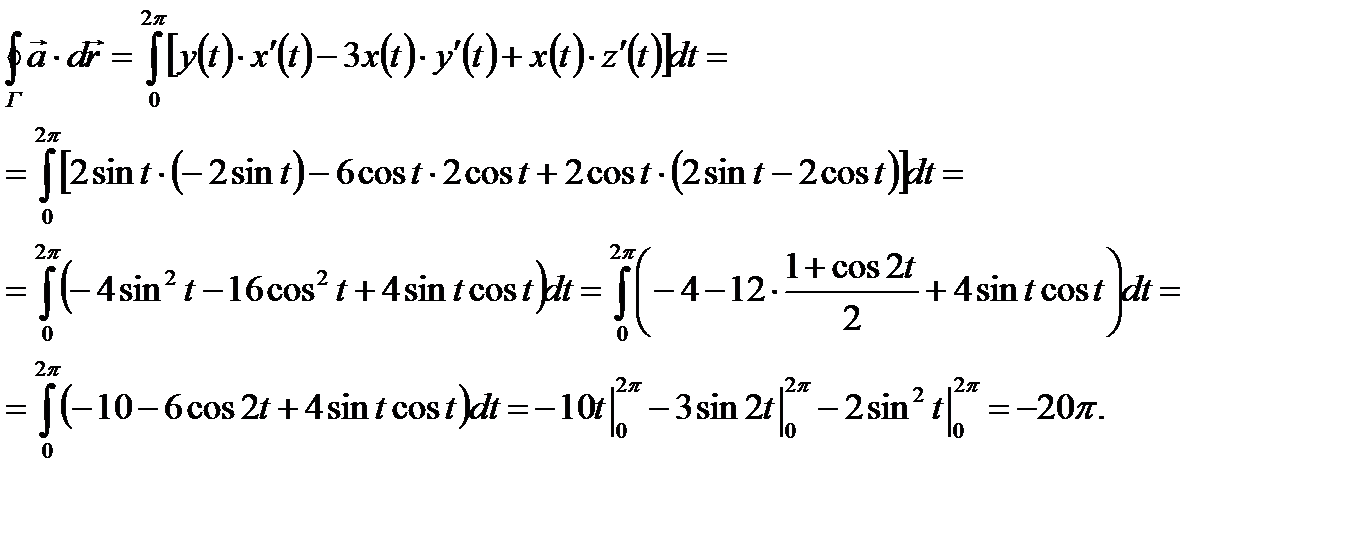
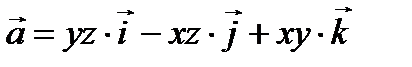 вдоль контура
вдоль контура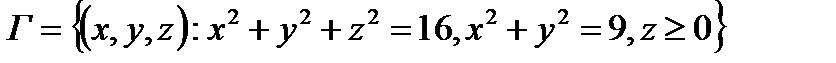 (см. рис. 10).
(см. рис. 10).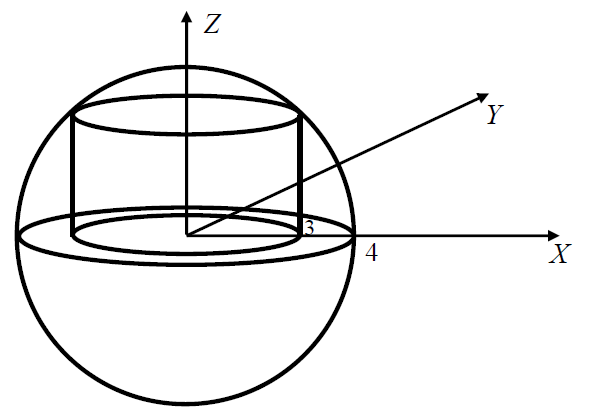
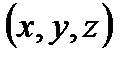 , лежащих на контуре Г, можно записать:
, лежащих на контуре Г, можно записать: 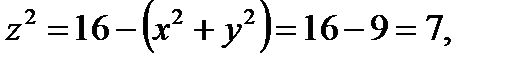 откуда, учитывая условие
откуда, учитывая условие 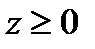 , получаем
, получаем 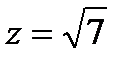 . Поскольку для точек кривой Г выполнено соотношение
. Поскольку для точек кривой Г выполнено соотношение 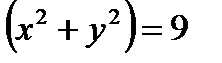 , на ней можно ввести параметризацию:
, на ней можно ввести параметризацию: 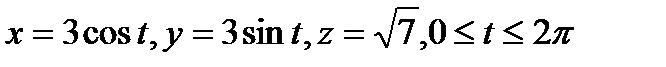 .
.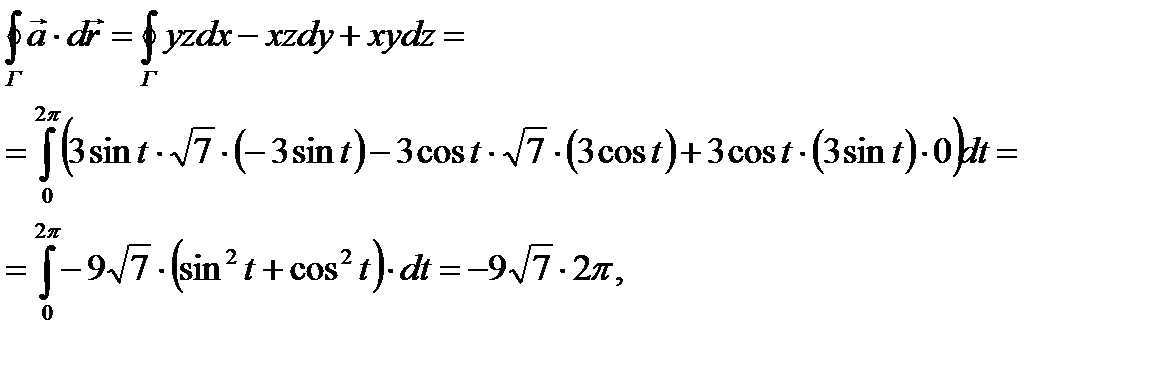
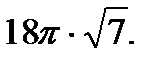
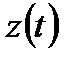 .
.


