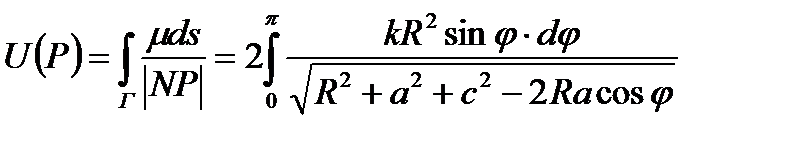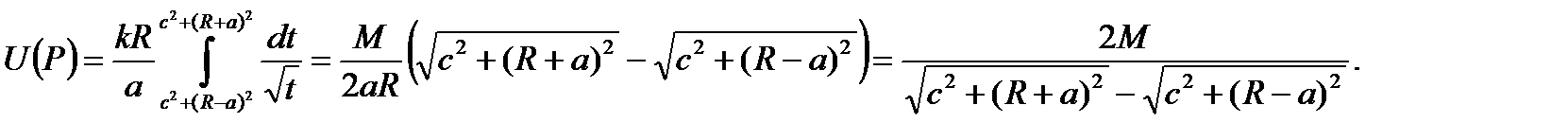Криволинейный интеграл первого рода от векторной функции.Обычно криволинейный интеграл вычисляется от скалярной функции f(x,y,z), т.е. скалярного поля, и назначением этого интеграла является число, т.е. тоже скаляр. Но в принципе, криволинейный интеграл первого рода можно находить и от векторной функции, т.е. от векторного поля. А именно, если в пространстве заданы кривая Г и векторное поле
то, по определению,
Понятно, что значение такого интеграла есть вектор.
Примеры на вычисление и приложения криволинейного интеграла первого рода. ПРИМЕР 1. Найти площадь поверхности, полученной вращением кривой Перейдем к полярным координатам:
В данном случае
По формуле (2), площадь поверхности вращения равна
Рис. 6. К примеру 1. Рис. 7. К примеру2.
ПРИМЕР 2. Вычислить ньютонов потенциал окружности Параметризуем окружность: (см. рис. 7):
Тогда, как легко проверить,
Плотность линии в точке N(x,y) равна
откуда Поэтому, по формуле (3), потенциал в точке P равен:
Для вычисления этого интеграла сделаем замену:
Тогда:
|
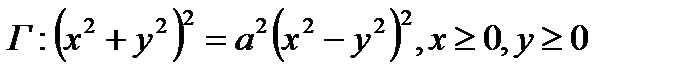, вокруг прямой 
.
получим: 
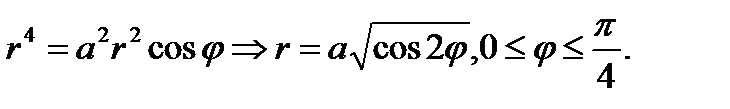Тогда кривая Г - это половина одной петли лемнискаты Бернулли (см. рис. 6). Расстояние от точки M(x,y) до прямой 
выражается формулой: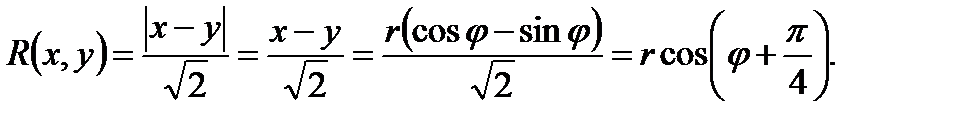
массой M в точке 
плотность в любой точке окружности пропорциональна расстоянию от этой точки до оси OX.
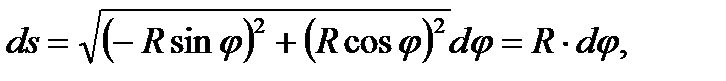
Найдем коэффициенты 
, для чего вычислим массу окружности:
.
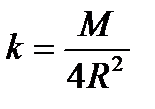