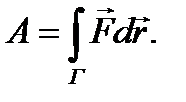Пусть на плоской кривой Г даны две произвольные точки  и
и  (см. рис. 12). Обозначим через
(см. рис. 12). Обозначим через  длину кривой между точками
длину кривой между точками  и
и  , через
, через 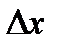 - абсциссу вектора
- абсциссу вектора  , а через
, а через  - его ординату. Из криволинейного треугольника
- его ординату. Из криволинейного треугольника  (см. рис. 14) по теореме Пифагора получаем:
(см. рис. 14) по теореме Пифагора получаем: 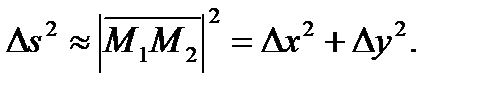 Пусть
Пусть  - угол между вектором
- угол между вектором  и осью абсцисс, а
и осью абсцисс, а  - угол между касательной к кривой Г в точке
- угол между касательной к кривой Г в точке  (предельным направлением вектора
(предельным направлением вектора  при
при  ) и положительным направлением оси. Тогда при
) и положительным направлением оси. Тогда при  имеем
имеем  . Кроме того, при малом значении
. Кроме того, при малом значении  можно считать, что
можно считать, что  . Поскольку
. Поскольку 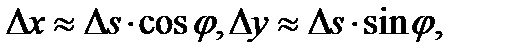 то при
то при  получаем:
получаем:


Рис. 12. К выводу формулы связи криволинейных
интегралов первого и второго рода.
В случае пространственной кривой касательная в точке  (предельное положение луча, направленного по вектору
(предельное положение луча, направленного по вектору  образует с координатными осями OX, OY, и OZ углы
образует с координатными осями OX, OY, и OZ углы  , соответственно, а вектор
, соответственно, а вектор  образует с теми же осями углы
образует с теми же осями углы  (см. рис. 13). При этом
(см. рис. 13). При этом

а  Тогда в пределе при
Тогда в пределе при  получаем:
получаем:

Подставив эти соотношения в интегральные суммы для криволинейных интегралов первого и второго рода, приходим при  (а значит, и
(а значит, и 
 ) к равенству соответствующих интегралов:
) к равенству соответствующих интегралов:

(1)
где  - функции точки М.
- функции точки М.

Рис. 13. К выводу формулы связи криволинейных
интегралов первого и второго рода.
Замечание. В двумерном случае (см. рис. 12) связь криволинейных интегралов первого и второго рода определяется формулой, аналогичной (1):

2.5. Физические приложения криволинейного интеграла второго рода.
Начнём с вопроса о работе силы  при перемещении материальной точки вдоль
при перемещении материальной точки вдоль
некоторой траектории. В самом простом случае, когда точка перемещается вдоль прямой, а сила направлена в сторону движения точки, работа равна модулю силы, умноженному на величину перемещения  . Если вектор
. Если вектор  составляет с направлением движения точки угол
составляет с направлением движения точки угол  , но сама сила постоянна, то
, но сама сила постоянна, то  , т.е. работа равна произведению тангенциальной составляющей силы на величину перемещения. То же самое можно записать в виде скалярного произведения
, т.е. работа равна произведению тангенциальной составляющей силы на величину перемещения. То же самое можно записать в виде скалярного произведения
(см. рис. 14).

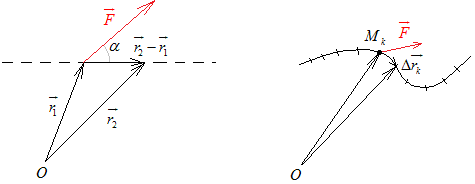
Рис. 14. Рис. 15.
Теперь предположим, что движение происходит не по прямой, а по криволинейной траектории, а сила зависит от положения материальной точки  .Чтобы сохранить предыдущие рассуждения, следует разбить траекторию на малые части,
.Чтобы сохранить предыдущие рассуждения, следует разбить траекторию на малые части,
причём каждую часть можно считать прямолинейной, а силу в пределах это части - постоянной, тогда на частичной дуге траектории работа силы равна  (см. рис.15). Точка может быть
(см. рис.15). Точка может быть  выбрана любая в пределах данной частичной дуги (в силу малости дуги сила не зависит от выбора этой точки). Чтобы получить работу силы на всей траектории, нужно суммировать работы на всех частичных дугах:
выбрана любая в пределах данной частичной дуги (в силу малости дуги сила не зависит от выбора этой точки). Чтобы получить работу силы на всей траектории, нужно суммировать работы на всех частичных дугах:

Чтобы равенство стало точным, следует перейти к пределу разбиения траектории на бесконечно малые части. Предел является криволинейным интегралом второго рода:
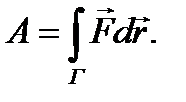

 и
и  (см. рис. 12). Обозначим через
(см. рис. 12). Обозначим через  длину кривой между точками
длину кривой между точками 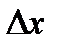 - абсциссу вектора
- абсциссу вектора  , а через
, а через  - его ординату. Из криволинейного треугольника
- его ординату. Из криволинейного треугольника  (см. рис. 14) по теореме Пифагора получаем:
(см. рис. 14) по теореме Пифагора получаем: 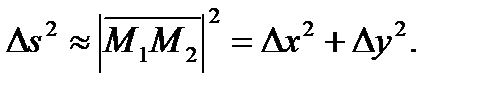 Пусть
Пусть  - угол между вектором
- угол между вектором  - угол между касательной к кривой Г в точке
- угол между касательной к кривой Г в точке  ) и положительным направлением оси. Тогда при
) и положительным направлением оси. Тогда при  . Кроме того, при малом значении
. Кроме того, при малом значении  . Поскольку
. Поскольку 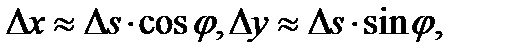 то при
то при 

 , соответственно, а вектор
, соответственно, а вектор  (см. рис. 13). При этом
(см. рис. 13). При этом
 Тогда в пределе при
Тогда в пределе при 
 (а значит, и
(а значит, и 
 ) к равенству соответствующих интегралов:
) к равенству соответствующих интегралов:
 - функции точки М.
- функции точки М.

 при перемещении материальной точки вдоль
при перемещении материальной точки вдоль . Если вектор
. Если вектор  , но сама сила постоянна, то
, но сама сила постоянна, то  , т.е. работа равна произведению тангенциальной составляющей силы на величину перемещения. То же самое можно записать в виде скалярного произведения
, т.е. работа равна произведению тангенциальной составляющей силы на величину перемещения. То же самое можно записать в виде скалярного произведения

 .Чтобы сохранить предыдущие рассуждения, следует разбить траекторию на малые части,
.Чтобы сохранить предыдущие рассуждения, следует разбить траекторию на малые части, (см. рис.15). Точка может быть
(см. рис.15). Точка может быть  выбрана любая в пределах данной частичной дуги (в силу малости дуги сила не зависит от выбора этой точки). Чтобы получить работу силы на всей траектории, нужно суммировать работы на всех частичных дугах:
выбрана любая в пределах данной частичной дуги (в силу малости дуги сила не зависит от выбора этой точки). Чтобы получить работу силы на всей траектории, нужно суммировать работы на всех частичных дугах: