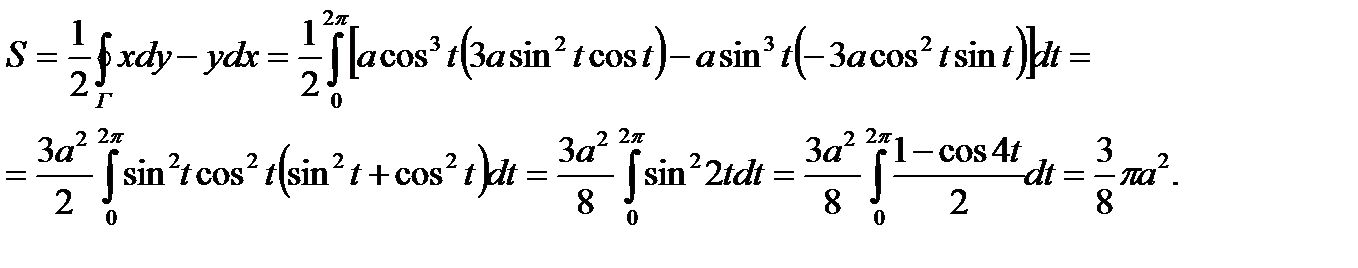Вычисление площади с помощью криволинейного интеграла второго рода.
В п.2.5.было установлено, что работа силового поля при перемещении материальной точки вдоль кривой Г выражается криволинейным интегралом второго рода по этой кривой. Применение криволинейного интеграла второго рода к решению физических задач будет изложено в теории поля. Покажем, что криволинейный интеграл может быть использован для вычисления площади плоской фигуры. Пусть D -некоторая область (правильная) с границей L и S - площадь этой области. Рассмотрим криволинейный интеграл
Аналогично получается другая формула
Можно получить иные формулы. Для этого достаточно выбрать функции
Так, если в интеграле
Следовательно,
(1) Формула (1) отличается от предыдущих двух симметричностью формы.
ПРИМЕР 1. Вычислить площадь области, ограниченной астроидой
Рис.16. К примеру 1.
Формула Грина.
Если D - односвязная область, то AD (граница области D) - простая замкнутая кривая, обход по которой совершается против часовой стрелки. Если D – неодносвязна, то AD - совокупность замкнутых кривых, обход по которым совершается так, что D остается слева.
|

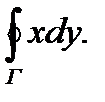 Применив к нему формулу Грина, где
Применив к нему формулу Грина, где  получим
получим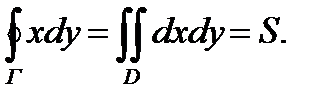

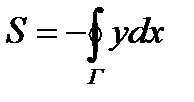
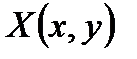 и
и  такими, чтобы они удовлетворяли условию
такими, чтобы они удовлетворяли условию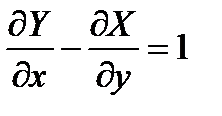
 положить
положить 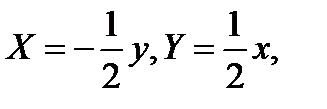 то
то  и
и

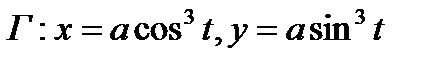 (см. рис.16). Применяя формулу (1), получим
(см. рис.16). Применяя формулу (1), получим