Введение. Количество гармонических составляющих входного несинусоидального напряжения по заданию:
Исходные данные: Количество гармонических составляющих входного несинусоидального напряжения по заданию: Амплитуды гармонических составляющих входного несинусоидального напряжения u1=f(ɷt), В
Частота основной гармонической входного напряжения, Гц: Параметры электрической цепи: -активные сопротивления, Ом: -индуктивности, мГн -емкости, мкФ
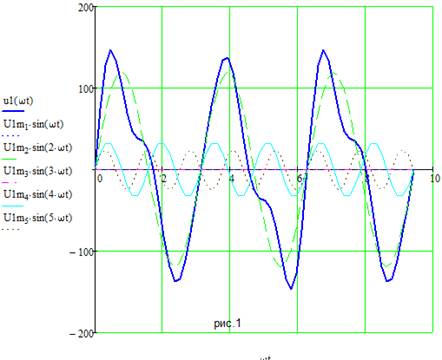
Представим входное воздействие u1(ɷt) в виде гармонического ряда
Круговая частота основной гармонической u1(ɷt), рад/с
На рис. Приведены графики заданных гармоник и суммарная кривая u1(ɷt) Определяем комплексный коэффициен передачи в общем виде. Введем мнимую единицу:
На рисунке приведены зависимости модуля и аргумента коэффициентов передачи для заданных гармоник u1(ɷt) Опрееляем амплитуды и начальные фазы заданных гармоник напряжения на выходе u2(ɷt)
Представим выходное напряжение u2(ɷt) в виде гармонического ряда
Определим действующее значение напряжения на нагрузке
График заданных гармоник и суммарная кривая М Введение Нам всем должно хорошо быть известно понятие от функции Оказывается, можно интегрировать функцию не только по прямолинейному отрезку координатной оси, но и вдоль любой линии AB на плоскости или в пространстве, которая может быть как прямолинейным отрезком, так и произвольной кривой. Такие интегралы называются криволинейными, или просто линейными. При это вычисление криволинейных интегралов сводится к вычислению определенных интегралов, а многие свойства и приложения криволинейных интегралов аналогичны соответствующим свойства определенных интегралов. Можно считать, что криволинейный интеграл - это обобщение понятия обычного определенного интеграла. Криволинейный интеграл теснейшим образом связан с важнейшими понятием в физике: работа силового поля вдоль некоторого пути. В данной курсовой работе даются все необходимые теоретические сведения относительно криволинейных интегралов, приведены их геометрические и физические приложения, разобраны иллюстрирующие примеры. Подробно освещается формула Грина и её применения.
|









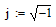





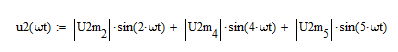


 на отрезке
на отрезке  , или, как еще говорят, по отрезку
, или, как еще говорят, по отрезку  , который обозначается
, который обозначается  Мы также должны хорошо помнить свойства определенных интегралов, методы их вычисления, геометрические физические приложения.
Мы также должны хорошо помнить свойства определенных интегралов, методы их вычисления, геометрические физические приложения.


