Непрерывно распределенные величины
Правило вычисления среднего непрерывно распределенной случайной величины можно получить, отправляясь от определения (15). Пусть случайная величина x принимает значения в интервале (xmin, xmax). Разобьем данный интервал на малые интервальчики длинами Dxk. Распределение вероятности приближенно опишется набором величин DPk, равных вероятностям того, что случайная величина x попадает в малый интервальчик под номером k. Тогда согласно (15) среднее значение величины x определится так: Одной из важных средних характеристик случайной величины является дисперсия. Она определяется следующей формулой: Для примера рассчитаем дисперсию x -проекции скорости молекулы в состоянии равновесия. Плотность распределения проекции скорости равна Вычисление сводится к математической процедуре, с которой полезно ознакомиться. Интеграл в правой части уравнения (24) имеет вид:
|

 (20)
(20)  (22)
(22) (22)
(22)  (23)
(23)  (24)
(24) (25)
(25)  (26)
(26)  (27)
(27)  (28)
(28)  (29)
(29) 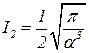 . (30)
. (30)  (31)
(31)  (32)
(32)


