Связь между вероятностью и энтропией состояния
Продолжим рассмотрение состояний газа как наиболее простой системы. В любом состоянии, вне зависимости от того, каким образом попал газ в это состояние - самопроизвольно или под действием внешних влияний - однозначно определена энтропия. А так как каждое состояние характеризуется вероятностью осуществления, должна иметь место связь между энтропией и вероятностью состояния.
Пусть объем сосуда равен 2V. Пусть также перемещение поршня совершалось столь медленно, что газ успевал принимать температуру окружающей среды (происходил квазистатический процесс). Тогда по закону Бойля-Мариотта Ключевое место. В данное состояние, полученное воздействием на газ поршнем, газ мог попасть случайно вследствие теплового движения молекул. Вероятность того, что этот процесс мог бы произойти сам, может быть вычислена по приближенной формуле, предложенной на предыдущем занятии -
Так как вероятность газу находиться в самом вероятном состоянии P(0) равна Используя (7), уравнение (9) можно переписать следующим образом:
Вернемся к способу насильственного перевода газа в состояние с неравными числами молекул в правой и левой половинах сосуда. Так как перемещение поршня производится изотермически, совершенная работа превращается в тепло. Часть тепла -Q1 передается в окружающую среду, а часть Q2 поглощает газ в расширяющемся отсеке. Ясно, что -Q1+Q2=A. При этом энтропия газа уменьшается на Уравнение (12) связывает между собой разность энтропий двух состояний и вероятности самопроизвольного пребывания газа в этих состояниях. Уравнение (12) записывают также в эквивалентном виде: Хотя соотношение (12) получено путем рассмотрения частной ситуации - распределение молекул газа по половинкам сосуда, на самом деле оно является общим и применимо для любой пары термодинамических состояний системы. Оно может быть использовано для вероятностного определения энтропии с точностью до множителя: Вывод: Чтобы перевести термодинамическую систему из более вероятного в менее вероятное состояние, надо совершить работу А, минимальное значение которой определяется разностью энтропий конечного и начального состояний:
Для примера рассмотрим сосуд с газом, разделенный пополам перегородкой. В одной половине газ, в другой - вакуум. Перегородку выдернули, предоставив газу распространяться по всему объему. Очевидно, что в первые мгновения после удаления перегородки вероятность того, что все молекулы будут находиться в одной половине сосуда близка к единице. С другой стороны, расчет вероятности такого состояния дает P=2-N, где N – число молекул в сосуде. Газ находится в маловероятном состояние. Противоречие?! На самом деле противоречия никакого нет. Рассчитанная вероятность P=2-N соответствует равновесному состоянию. А состояние газа после выдергивания перегородки не является равновесным. Газ не будет продолжать в нем оставаться. Он самопроизвольно будет переходить в более вероятное состояние - молекулы равномерно распределятся по всему объему сосуда. Вернемся к одной из формулировок второго начала термодинамики, в которой говорится, что любая термодинамическая система самопроизвольно переходит в состояние теплового равновесия, в котором ее энтропия максимальна. Из проведенного выше рассмотрения становится ясным вероятностный смысл второго начала. Оно просто-напросто утверждает, что термодинамическая система самопроизвольно переходит в наиболее вероятное состояние. Величина энтропии характеризует вероятность термодинамического состояния. Все содержание второго начала сводится к очевидному утверждению: “Систему вероятнее обнаружить в более вероятном состоянии”. Заметим, из данной формулировки не следует, что попадание в маловероятное состояние невозможно. Второе начало только утверждает, что посещение маловероятных состояний является редким событием. Самопроизвольный переход в более вероятное состояние (в состояние с большей энтропией) происходит только в том случае, если имеется канал перехода. Так, более вероятное состояние, в котором молекулы в равных половинках сосуда распределены поровну, недостижимо, когда половинки разделены перегородкой. Канал перехода закрыт. Переход возможен только после удаления перегородки. Каналы переходов могут быть перекрыты из-за действия законов сохранения.
|


 В качестве примера нахождения связи между вероятностью термодинамического состояния и энтропией рассмотрим одноатомный идеальный газ. Пусть он находится в самом вероятном состоянии: в каждой половине сосуда поровну (по N ) молекул. Установим в сосуде поршень и отделим его часть, в которой находится N+n молекул, от другой, в которой N–n молекул. Затем изотермически переместим поршень так, чтобы он разделил сосуд точно пополам. Получилось так, что захватив в правой половине n молекул, мы перевели их в левую половину. При этом придется совершить работу по перемещению поршня. Совершив работу, мы перевели газ в новое состояние, в котором при равных объемах в левой половине N+n молекул, а в правой N-n.
В качестве примера нахождения связи между вероятностью термодинамического состояния и энтропией рассмотрим одноатомный идеальный газ. Пусть он находится в самом вероятном состоянии: в каждой половине сосуда поровну (по N ) молекул. Установим в сосуде поршень и отделим его часть, в которой находится N+n молекул, от другой, в которой N–n молекул. Затем изотермически переместим поршень так, чтобы он разделил сосуд точно пополам. Получилось так, что захватив в правой половине n молекул, мы перевели их в левую половину. При этом придется совершить работу по перемещению поршня. Совершив работу, мы перевели газ в новое состояние, в котором при равных объемах в левой половине N+n молекул, а в правой N-n.
 После перемещения поршня в левой половине сосуда давление повысится до P1, а в правой - понизится до P2. В конечном состоянии на поршень будет действовать сила (P1-P2)S, где S - площадь поршня. При малом смещении поршня можно считать, что разность сил давления линейно изменялась от нуля до максимального значения, поэтому при перемещении придется совершить работу
После перемещения поршня в левой половине сосуда давление повысится до P1, а в правой - понизится до P2. В конечном состоянии на поршень будет действовать сила (P1-P2)S, где S - площадь поршня. При малом смещении поршня можно считать, что разность сил давления линейно изменялась от нуля до максимального значения, поэтому при перемещении придется совершить работу  (1)
(1) 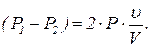 (3)
(3)  (4)
(4) 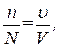 (5)
(5) 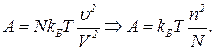 (7)
(7) (8)
(8)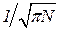 , то
, то  (9)
(9) (10)
(10) 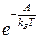 от вероятности самого вероятного распределения молекул. Здесь A - работа, которую надо было бы произвести, чтобы осуществить переход из наивероятнейшего состояния в заданное путем внешнего воздействия.
от вероятности самого вероятного распределения молекул. Здесь A - работа, которую надо было бы произвести, чтобы осуществить переход из наивероятнейшего состояния в заданное путем внешнего воздействия.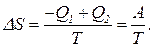 (11)
(11) 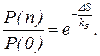 (12)
(12)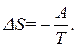 (14)
(14)  Как известно, работа, совершенная над системой в адиабатическом процессе, равна изменению энергии при переходе системы из одного состояния в другое: A=E2-E1. Поэтому отношение вероятностей P(E1) и P(E2) пребывания системы в состоянии с энергиями E1 и E2 можно записать в виде:
Как известно, работа, совершенная над системой в адиабатическом процессе, равна изменению энергии при переходе системы из одного состояния в другое: A=E2-E1. Поэтому отношение вероятностей P(E1) и P(E2) пребывания системы в состоянии с энергиями E1 и E2 можно записать в виде:  (15)
(15) 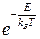 :
:  (16)
(16) 


