Плотность распределения f(x) локализована в некоторой ограниченной области определения, например так, как показано на рисунке. Как известно, фурье-образ w(k) локализованной функции представляет собой также локализованную функцию. А поскольку фурье-образ распределения F(Z) равен степени wm(k) с большим показателем m, скорость спадания ее  от максимума к нулю гораздо больше, чем скорость спадания w(k). Это означает, что в обратном преобразовании
от максимума к нулю гораздо больше, чем скорость спадания w(k). Это означает, что в обратном преобразовании
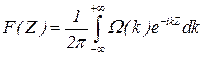
 (42)
(42)
главный вклад в интеграл дает малая область значений k вблизи нуля. Поэтому величину w(k)=exp{ln w(k)}
преобразуем так: разложим ln w(k) в ряд по степеням k и ограничимся только членами до квадратичного:
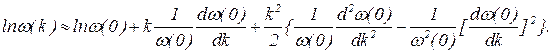 Заметим, что
Заметим, что
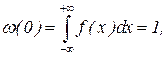 (43)
(43)
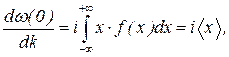 (44)
(44)
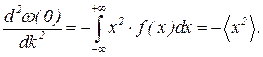 (45)
(45)
Суммируя все вместе, получаем
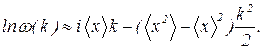 (46)
(46)
Производящая функция плотности распределения суммы равна
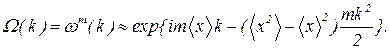 (47)
(47)
Проведем обратное преобразование (42). Оно дает
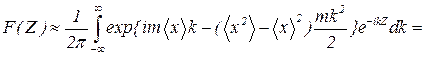
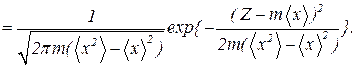 (48)
(48)
Из формулы (48) следует, что сумма m случайных величин распределена по гауссовскому закону со средним равным сумме средних значений слагаемых и с дисперсией равной сумме дисперсий. Отсюда в частности следует, что если складывается N случайных величин с ненулевым средним, как, например, сила давления молекул газа на стенку сосуда, то относительный разброс суммы убывает с ростом N пропорционально N-1/2.
Практическое занятие №8

 от максимума к нулю гораздо больше, чем скорость спадания w(k). Это означает, что в обратном преобразовании
от максимума к нулю гораздо больше, чем скорость спадания w(k). Это означает, что в обратном преобразовании 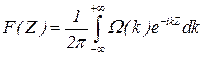
 (42)
(42) 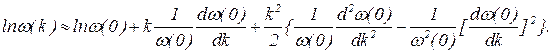 Заметим, что
Заметим, что 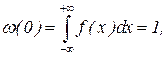 (43)
(43) 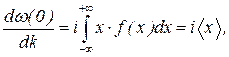 (44)
(44) 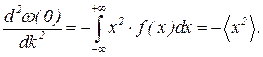 (45)
(45) 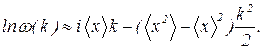 (46)
(46) 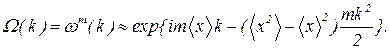 (47)
(47)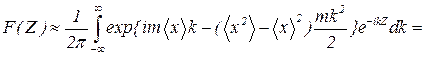
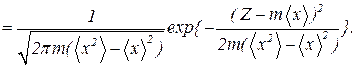 (48)
(48)


