При решении любой из задач, в которых приходится находить распределение вероятности, желательно включать процедуру определения поля элементарных событий и распределения вероятности на поле элементарных событий (см. пример решения задачи 3).
Задача 1. Какова вероятность выпадания шестерки или меньшего числа при трех бросаниях игральной кости?
Задача 2. Рассмотрим случайные числа между 0 и 1. Чему равна вероятность того, что ровно пять из десяти мест после запятой заняты цифрами, меньшими 5?
Задача 3. Предположим, что все грани игральной кости выпадают с одинаковой вероятностью. Рассмотрим игру, которая заключается в выбрасывании сразу пяти костей. Найдите вероятность выпадения шестерки:
а) ровно в одной кости,
б) по крайней мере в одной кости,
в) в двух костях.
Решение. Элементарнымсобытием является определенная раскладка очков на гранях каждой кости, например { 3, 1, 1, 2, 5 } или { 6, 2, 4, 3, 2 } и т.п. Поле элементарных событий состоит из 65 =7776 элементов. Из соображений симметрии элементарные события равновероятны. Вероятность каждого события равна 1/65=6-5.
а) Событие, заключающееся в выпадения шестерки ровно в одной кости, представляет собой сложное событие. Оно включает в себя 54 распределений, в которых шестерка выпала на кости №1 такого типа { 6, x2, x3, x4, x5 }, где x2, x3, x4, x5¹6. Еще столько же в него входят элементарных событий, в которых шестерка выпала на кости №2, еще столько же в него входят элементарных событий, в которых шестерка выпала на третьей кости и т.д. Таким образом, данное сложное событие включает в себя 6×54 элементарных событий. Вероятность осуществления равна сумме вероятностей всех элементарных событий, составляющих его, т.е. Pa=5×54×6-5=(5/6)5»0,402.
б) Для ответа на вопрос б проще подсчитать вероятность невыпадения ни одной шестерки. Число элементарных событий вида { x1, x2, x3, x4, x5 }, где x1, x2, x3, x4, x5¹6, входящих в сложное событие “среди пяти костей нет ни одной, на которой была бы шестерка” равно 55. Значит, число элементарных событий, составляющих искомое, равно 65-55,вероятность такого события равна (65-55)×6-5=1-(5/6)5» 0,598.
в) Элементарные события, в которых ровно на двух костях выпали шестерки, имеют вид такого типа - { x1, 6, x3, 6, x5 }. На каждую пару шестерок приходится 53 распределений на остальных трех костях, не содержащих ни одной шестерки. Всего размещений двух костей с шестерками по номерам костей равно 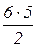 , поэтому полное число элементарных событий, в которых ровно на двух костях выпали шестерки, равно
, поэтому полное число элементарных событий, в которых ровно на двух костях выпали шестерки, равно 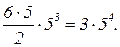 ×С учетом равновероятности всех элементарных событий находим вероятность:
×С учетом равновероятности всех элементарных событий находим вероятность:
Pв=3×54×6-5=(1/2)×(5/6)4» 0,241.
Задача 4. Русская рулетка. В шестизарядный барабан револьвера вкладывается один боевой патрон. Затем барабан вращают и стреляют в себя. Какова вероятность остаться в живых после:
а) одного испытания?
б) двух испытаний?
в) N испытаний?
г) какова вероятность быть застреленным при N испытаниях?
Задача 5. Совершенно пьяный человек начинает свое движение от фонаря посреди улицы, делая шаги равной длины b. Вероятность того, что он сделает шаг вправо, равна p, а вероятность сделать шаг влево равна q=1-p. Человек настолько пьян, что, делая данный шаг, он совершенно не помнит о направлении предыдущего. Таким образом, его шаги статистически независимы. Предположим, что он сделал N шагов.
а) Какова вероятность P(n) того, что n шагов будет сделано вправо, а остальные N-n шагов влево?
б) Какова вероятность P`(m) того, что человек удалится от фонаря на расстояние mb (m - целое число)?
Задача рассмотрена на лекции.
Задача 6. Допустим, что в предыдущей задаче q=p, так что вероятности смещения влево и вправо при каждом шаге равны. Какова вероятность того, что после N шагов человек возвратится к фонарю?
Задача 7. Одномерная диффузия атома. Вдоль оси OX натянута тонкая медная проволока. Несколько атомов меди, расположенные вблизи x=0, радиоактивны (предположим, например, что их бомбардировали нейтронами). При увеличении температуры нити подвижность атомов возрастает. При этом каждый атом может перескочить на соседнее место кристаллической решетки либо направо (в направлении +x), либо налево (в направлении - x). Соседние места в решетке разделены расстояниями b. Предположим, что время нахождения атома в данном узле решетки равно t. Время t является быстро убывающей функцией термодинамической температуры решетки.
Предположим, что в момент времени t=0 температура нити быстро возрастает до некоторого большого значения и в дальнейшем остается неизменной.
а) Обозначим через P(x)dx вероятность того, что радиоактивный атом будет обнаружен по истечении времени t в интервале от x до x+dx. (Мы предполагаем, что t>>t для всех значений t, представляющих физический интерес, так как при высокой температуре нити t достаточно мало.) Изобразите на графике примерный ход P(x) в зависимости от x для следующих трех случаев: 1) вскоре после t=0; 2) по прошествии времени t>>t, но недостаточного для достижения атомами концов проволоки; 3) по прошествии очень большого времени.
б) Чему равно среднее смещение радиоактивного атома за время t?
в) Получите формулу для среднеквадратичного (стандартного) отклонения Dx радиоактивного атома за время t.
Задача 8. Используя общие свойства вычисления среднего, покажите, что дисперсия случайной величины u может быть вычислена по формуле:
á Du2 ñ = á(u – u ñ) 2 ñ = á u2 - á u ñ 2 ñ.
Покажите, что из данного равенства следует общее неравенство:
á u2 ñ ³;á u ñ 2. (2)
Задача 9. Рассмотрим частицу со спином, равным ћ/2. Ее магнитный момент m с вероятностью p может быть ориентирован по магнитному полю B и с вероятностью q=1-p - против поля. В первом случае проекция магнитного момента на поле равна +m0, а во втором она равна -m0.
а) Найдите, чему равны á m ñ иá m2 ñ.
б) Вычислите á Dm2 ñ.
Задача 10 [ C5.8.1 ]. а) Разделим сосуд вместимости V на две равные части 1 и 2. Пусть в этом сосуде движется одна молекула. Будем наблюдать за ней в течение времени t. В среднем половину этого времени молекула будет находиться в части 1 сосуда, а половину в части 2.
а) В течение какого времени в части 1 вместе с первой будет находиться вторая молекула, если в сосуде движутся две молекулы?
б) В сосуде движутся три молекулы. В течение какого времени они будут находиться одновременно в части 1?
в) В сосуде движутся N молекул. В течение какого времени они будут находиться одновременно в части 1?
Задача 11. Флуктуации плотности в газе. Рассмотрим идеальный газ из N молекул, находящийся в тепловом равновесии в сосуде объемом V0. Обозначим через n число молекул, находящихся в какой-то части объема V Вероятность того, что отдельная молекула находится в выделенной части объема равна p=V / V0.
а) Чему равно среднее число молекулá n ñ в части объема V? Выразите ваш ответ через N, V, V0.
б) Чему равно среднеквадратичное отклонение числа молекул Dn =á n2- á n ñ 2 ñ 1/2 в части объема V? Найдите Dn/n. Выразите ответ через N, V, V0.
в) Получите приближенную формулу при V<<V0.
г) К чему стремится среднеквадратичное отклонение числа молекул Dn =á n2- á n ñ 2 ñ 1/2 в части объема V при V ® V0?
Задача 12 [ C5.8.3 ]. В сосуде объемом V0 находятся N молекул.
а) Определите вероятность того, что в объеме V<V0, который представляет собой часть объема V0, не будет ни одной молекулы?
б) Чему будет равен объем, при котором вероятность такого события близка к 10-2?
Решение. Какбыло показано на лекции, распределение молекул в сосуде с выделенным объемом V описывается биномиальной формулой
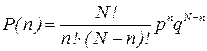 (3)
(3)
где P(n) - вероятность того, что в выделенном объеме находятся n молекул, p=V/V0, q=1-p.
а) Применяя формулу (3) к исследуемой ситуации, находим:
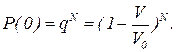 (4)
(4)
При V<<V0 и N>>1 можно получить приближенное выражение. Введем объемную плотность частиц n=N/V0. При этом формула (4) принимает вид:
 (5)
(5)
б) Используем последнее уравнение
 , (6)
, (6)
где v 0 – среднее значение объема, приходящегося на одну молекулу.

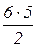 , поэтому полное число элементарных событий, в которых ровно на двух костях выпали шестерки, равно
, поэтому полное число элементарных событий, в которых ровно на двух костях выпали шестерки, равно 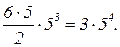 ×С учетом равновероятности всех элементарных событий находим вероятность:
×С учетом равновероятности всех элементарных событий находим вероятность: 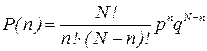 (3)
(3) 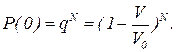 (4)
(4)  (5)
(5)  , (6)
, (6) 


