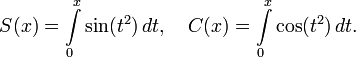Функция распределения нормируется условием  .
.
Такая нормировка называется нормировкой на единицу. Если в системе имеется  одинаковых объектов, справа вместо 1 иногда ставят число
одинаковых объектов, справа вместо 1 иногда ставят число  . Тогда говорят, что функция распределения нормирована на «число частиц». Правило вычисления средних статистических величин: Вначале записывают тождество
. Тогда говорят, что функция распределения нормирована на «число частиц». Правило вычисления средних статистических величин: Вначале записывают тождество  , где
, где  – та физическая величина, которую надо сопоставлять с экспериментом, или функциональные зависимости которой от разных параметров надо исследовать. Тождество интегрируют с функцией распределения (оно остается тождеством):
– та физическая величина, которую надо сопоставлять с экспериментом, или функциональные зависимости которой от разных параметров надо исследовать. Тождество интегрируют с функцией распределения (оно остается тождеством):  . Интегрирование проводится по всем допустимым значениям Х. Затем предполагается, что в первом интеграле стоит не сам оператор
. Интегрирование проводится по всем допустимым значениям Х. Затем предполагается, что в первом интеграле стоит не сам оператор  , а его среднее статистическое значение
, а его среднее статистическое значение  , которое является независящей от Х константой. Константу вынести из под интеграла,
, которое является независящей от Х константой. Константу вынести из под интеграла,  . Поскольку функция распределения предполагается нормированной на единицу, стоящий слева интеграл равен 1 и мы получает формулу для расчета среднего
. Поскольку функция распределения предполагается нормированной на единицу, стоящий слева интеграл равен 1 и мы получает формулу для расчета среднего  .
.
19) Распределение Максвелла для одномерного движения частиц. Интеграл Френеля. Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию.
Интегралы Френеля S(x) и C(x) — это специальные функции, названные в честь Огюстена Жана Френеля и используемые в оптике. Они возникают при расчёте дифракции Френеля и определяются как 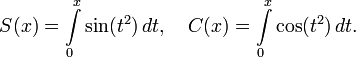

 .
. одинаковых объектов, справа вместо 1 иногда ставят число
одинаковых объектов, справа вместо 1 иногда ставят число  , где
, где  – та физическая величина, которую надо сопоставлять с экспериментом, или функциональные зависимости которой от разных параметров надо исследовать. Тождество интегрируют с функцией распределения (оно остается тождеством):
– та физическая величина, которую надо сопоставлять с экспериментом, или функциональные зависимости которой от разных параметров надо исследовать. Тождество интегрируют с функцией распределения (оно остается тождеством):  . Интегрирование проводится по всем допустимым значениям Х. Затем предполагается, что в первом интеграле стоит не сам оператор
. Интегрирование проводится по всем допустимым значениям Х. Затем предполагается, что в первом интеграле стоит не сам оператор  , которое является независящей от Х константой. Константу вынести из под интеграла,
, которое является независящей от Х константой. Константу вынести из под интеграла,  . Поскольку функция распределения предполагается нормированной на единицу, стоящий слева интеграл равен 1 и мы получает формулу для расчета среднего
. Поскольку функция распределения предполагается нормированной на единицу, стоящий слева интеграл равен 1 и мы получает формулу для расчета среднего  .
.