Теперь нормированную на число частиц функцию распределения Максвелла по скоростям в случае одномерного движения можно записать в виде:  . Позже это распределение было проверено экспериментально и получило хорошее подтверждение в опытах Штерна и Герлаха.
. Позже это распределение было проверено экспериментально и получило хорошее подтверждение в опытах Штерна и Герлаха.
Напомним, что рассматривалось одномерное движение. Для рассмотрения трехмерного движения надо вспомнить, что в силу независимости движения по ортогональным осям координат 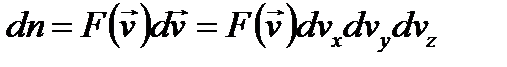 и опять провести нормировку на число частиц:
и опять провести нормировку на число частиц:
 . Здесь перемножаются три одинаковых интеграла типа
. Здесь перемножаются три одинаковых интеграла типа 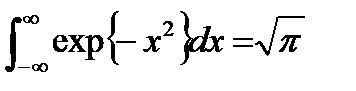 , так что новая постоянная нормировки
, так что новая постоянная нормировки  .
.
Значит, в случае трехмерного движения функция распределения Максвелла имеет вид  .
.
Уместно замечание о том, что в настоящее время чаще используют распределение не по скоростям, а по импульсам (тогда это распределение можно использовать в релятивистских задачах):  . Эта функции распределения относится к случаю прямоугольной Декартовой системы координат. Однако часто удобнее использовать сферическую систему координат, считая, что
. Эта функции распределения относится к случаю прямоугольной Декартовой системы координат. Однако часто удобнее использовать сферическую систему координат, считая, что  , при этом по телесному углу
, при этом по телесному углу  можно проинтегрировать, что дает множитель
можно проинтегрировать, что дает множитель  , и тогда
, и тогда  можно заменить множителем
можно заменить множителем  . Функция распределения в этом случае зависит от модуля скорости, изменяющемся в интервале
. Функция распределения в этом случае зависит от модуля скорости, изменяющемся в интервале  . Такая функция называется функцией распределения Максвелла по модулям скоростей и имеет вид:
. Такая функция называется функцией распределения Максвелла по модулям скоростей и имеет вид:  .
.
Функцию распределения по модулям скоростей можно изобразить графиком (см. рис. 9)
| Рис. 9. Распределение Максвелла
модулям скоростей.
|
На рисунке 9 приближенное изображение функции распределения Максвелла для некоторой температуры T. Точка А – точка касания горизонтальной прямой – максимум функции  . Этой точке соответствует наиболее вероятная скорость. Площадь под кривой определяет условие нормировки (1 или N). При повышении температуры максимум сдвигается вправо, становясь ниже, так что нормировка и площадь под кривой сохраняются.
. Этой точке соответствует наиболее вероятная скорость. Площадь под кривой определяет условие нормировки (1 или N). При повышении температуры максимум сдвигается вправо, становясь ниже, так что нормировка и площадь под кривой сохраняются.
При изучении распределения Максвелла по скоростям Больцман заметил, что в показателе экспоненты стоит отношение кинетической энергии к энергии  . Это послужило основанием для обобщения распределения на случай, когда частица имеет потенциальную энергию. Такое распределение часто называют распределением Больцмана. В этом случае функция распределения может быть записана в виде:
. Это послужило основанием для обобщения распределения на случай, когда частица имеет потенциальную энергию. Такое распределение часто называют распределением Больцмана. В этом случае функция распределения может быть записана в виде:  , где нормировка проводится по всем координатам, либо по указанной координатной области. Например, если рассматривается изотермическая атмосфера, находящаяся в равновесии, и потенциальная энергия частиц ансамбля равна:
, где нормировка проводится по всем координатам, либо по указанной координатной области. Например, если рассматривается изотермическая атмосфера, находящаяся в равновесии, и потенциальная энергия частиц ансамбля равна: 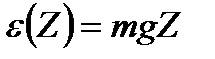 , где Z – высота над уровнем моря, то тогда
, где Z – высота над уровнем моря, то тогда 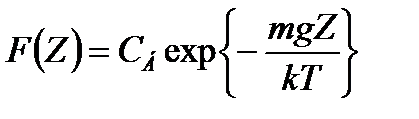 . Нормировка может проводиться на плотность частиц в единице объема (на концентрацию частиц
. Нормировка может проводиться на плотность частиц в единице объема (на концентрацию частиц  ) или на давление P(Z). Тогда говорят о барометрических распределениях, имеющих вид:
) или на давление P(Z). Тогда говорят о барометрических распределениях, имеющих вид:
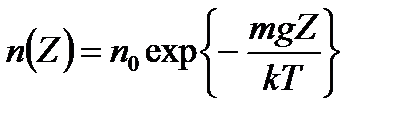 ,
,  .
.
Величины, имеющие индексы «0» – отмечают значения на уровне моря.
Аналогичным образом можно записать распределение гармонических осцилляторов по энергиям. Если считать, что энергия осциллятора равна:  , то соответствующая функция распределения имеет вид:
, то соответствующая функция распределения имеет вид:  . Например, если рассматривается изотермическая атмосфера, находящаяся в равновесии, и потенциальная энергия частиц ансамбля равна:
. Например, если рассматривается изотермическая атмосфера, находящаяся в равновесии, и потенциальная энергия частиц ансамбля равна: 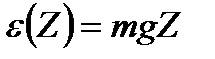 , где Z – высота над уровнем моря, то тогда
, где Z – высота над уровнем моря, то тогда 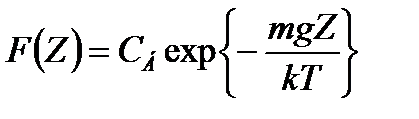 . Нормировка может проводиться на плотность частиц в единице объема (на концентрацию частиц
. Нормировка может проводиться на плотность частиц в единице объема (на концентрацию частиц  ) или на давление P(Z). Тогда говорят о барометрических распределениях, имеющих вид
) или на давление P(Z). Тогда говорят о барометрических распределениях, имеющих вид 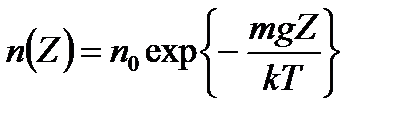 ,
,  . Величины, имеющие индексы «0» – отмечают значения на уровне моря.
. Величины, имеющие индексы «0» – отмечают значения на уровне моря.

 . Позже это распределение было проверено экспериментально и получило хорошее подтверждение в опытах Штерна и Герлаха.
. Позже это распределение было проверено экспериментально и получило хорошее подтверждение в опытах Штерна и Герлаха.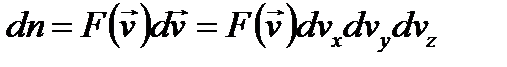 и опять провести нормировку на число частиц:
и опять провести нормировку на число частиц: . Здесь перемножаются три одинаковых интеграла типа
. Здесь перемножаются три одинаковых интеграла типа 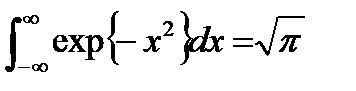 , так что новая постоянная нормировки
, так что новая постоянная нормировки  .
. .
. . Эта функции распределения относится к случаю прямоугольной Декартовой системы координат. Однако часто удобнее использовать сферическую систему координат, считая, что
. Эта функции распределения относится к случаю прямоугольной Декартовой системы координат. Однако часто удобнее использовать сферическую систему координат, считая, что  , при этом по телесному углу
, при этом по телесному углу  можно проинтегрировать, что дает множитель
можно проинтегрировать, что дает множитель  , и тогда
, и тогда  можно заменить множителем
можно заменить множителем  . Функция распределения в этом случае зависит от модуля скорости, изменяющемся в интервале
. Функция распределения в этом случае зависит от модуля скорости, изменяющемся в интервале  . Такая функция называется функцией распределения Максвелла по модулям скоростей и имеет вид:
. Такая функция называется функцией распределения Максвелла по модулям скоростей и имеет вид:  .
.

 . Этой точке соответствует наиболее вероятная скорость. Площадь под кривой определяет условие нормировки (1 или N). При повышении температуры максимум сдвигается вправо, становясь ниже, так что нормировка и площадь под кривой сохраняются.
. Этой точке соответствует наиболее вероятная скорость. Площадь под кривой определяет условие нормировки (1 или N). При повышении температуры максимум сдвигается вправо, становясь ниже, так что нормировка и площадь под кривой сохраняются. . Это послужило основанием для обобщения распределения на случай, когда частица имеет потенциальную энергию. Такое распределение часто называют распределением Больцмана. В этом случае функция распределения может быть записана в виде:
. Это послужило основанием для обобщения распределения на случай, когда частица имеет потенциальную энергию. Такое распределение часто называют распределением Больцмана. В этом случае функция распределения может быть записана в виде:  , где нормировка проводится по всем координатам, либо по указанной координатной области. Например, если рассматривается изотермическая атмосфера, находящаяся в равновесии, и потенциальная энергия частиц ансамбля равна:
, где нормировка проводится по всем координатам, либо по указанной координатной области. Например, если рассматривается изотермическая атмосфера, находящаяся в равновесии, и потенциальная энергия частиц ансамбля равна: 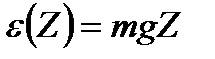 , где Z – высота над уровнем моря, то тогда
, где Z – высота над уровнем моря, то тогда 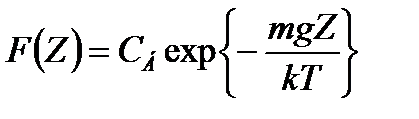 . Нормировка может проводиться на плотность частиц в единице объема (на концентрацию частиц
. Нормировка может проводиться на плотность частиц в единице объема (на концентрацию частиц  ) или на давление P(Z). Тогда говорят о барометрических распределениях, имеющих вид:
) или на давление P(Z). Тогда говорят о барометрических распределениях, имеющих вид: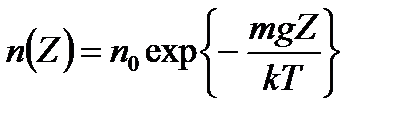 ,
,  .
. , то соответствующая функция распределения имеет вид:
, то соответствующая функция распределения имеет вид:  . Например, если рассматривается изотермическая атмосфера, находящаяся в равновесии, и потенциальная энергия частиц ансамбля равна:
. Например, если рассматривается изотермическая атмосфера, находящаяся в равновесии, и потенциальная энергия частиц ансамбля равна: 


