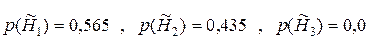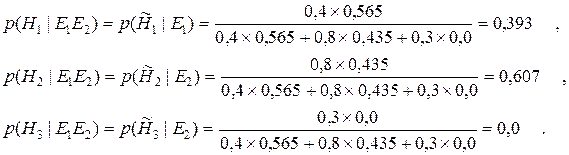Последовательное распространение вероятностей

Однако реально, распространение вероятностей происходит поэтапно с суммированием отдельных свидетельств и их влияния на условную вероятность по мере поступления отдельных E_i. Это можно сделать, используя априорные и апостериорные вероятности, следующим образом:

1. Задаём p(H_i) – априорную вероятность событий H_i.

2. Для полученных свидетельств E_j записываем p(E_j | H_i).

3. С учётом теоремы Байеса подсчитываем p(H_i | E_j) в зависимости от исхода E_j, то есть вычисляем апостериорную вероятность события H_i.

4. Теперь можно не обращать внимания на все наступившие E_j и переобозначить текущую апостериорную вероятность события H_i, как новую априорную вероятность H_i. Итак, пусть p(H_i) равна p(H_i | E_j) в зависимости от значения E_j.

5. Затем выберем новое свидетельство для рассмотрения и перейдём к п.2.

Проиллюстрируем эту последовательность на приведенном выше примере в предположении, что сначала поступило свидетельство E₂. Тогда:

Полученные вероятности можно принять за новые апостериорные вероятности гипотез H₁, H₂, и H₃, то есть:

И если теперь дополнительно поступит свидетельство E₂, то новые апостериорные вероятности гипотез могут быть вычислены только на основе вновь поступившего свидетельства:

Из приведенного примера видно, что итерационная процедура последовательного распределения вероятностей по мере поступления свидетельств позволяет получить результаты аналогичные непосредственному применению правила Байеса для случая одновременного двух поступивших свидетельств.