Простейший логический вывод

Рассмотрим случай, когда все правила в экспертной системе отражаются в форме:

 

Если < H является истинной > То < E будет наблюдаться с вероятностью р >;.

 

Очевидно, если H произошло, то это правило говорит о том, что событие E происходит с вероятностью p. Но что будет, если состояние H неизвестно, а E произошло? Использование теоремы Байеса позволяет вычислить вероятность того, что H истинно. Замена «A» и «B» на «H» и «E» не существенна для формулы Байеса, но с её помощью мы можем покинуть общую теорию вероятности и перейти к анализу вероятностных вычислений в ЭС. В этом контексте:

· H – событие, заключающееся в том, что данная гипотеза верна;

· E – событие, заключающееся в том, что наступило определённое доказательство (свидетельство), которое может подтвердить правильность указанной гипотезы.

Переписывая формулу Байеса в терминах гипотез и свидетельств, получим:

.

Это равенство устанавливает связь гипотезы со свидетельством и, в то же время, наблюдаемого свидетельства с пока ещё не подтверждённой гипотезой. Эта интерпретация предполагает также определение априорной вероятности гипотезы p(H), назначаемой H до наблюдения или получения некоторого факта.

В экспертных системах вероятности, требуемые для решения некоторой проблемы, обеспечивается экспертами и запоминается в базе знаний. Эти вероятности включают:

· априорные вероятности всех возможных гипотез p(H);

· условные вероятности возникновения свидетельств при условии существования каждой из гипотез p(E | H).

Так, например, в медицинской диагностике эксперт должен задать априорные вероятности всех возможных болезней в некоторой медицинской области. Кроме того, должны быть определены условные вероятности проявления тех или иных симптомов при каждой из болезней. Условные вероятности должны быть получены для всех симптомов и болезней, предполагая, что все симптомы независимы в рамках одной болезни.

Два события E₁ и E₂ являются условно независимыми, если их совместная вероятность при условии некоторой гипотезы H равна произведению условных вероятностей эти событий при условии H, то есть

p(E₁ E₂ | H) = p(E₁ | H) × p(E₂ | H).

Пользователи дают ЭС информацию о наблюдениях (наличии определённых симптомов) и ЭС вычисляет p(H_i | E_j... E_k) для всех гипотез (H₁,..., H_m) в свете предъявленных симптомов (E_j,..., E_k) и вероятностях, хранимых в БЗ.

Вероятность p(H_i | E_j... E_k) называется апостериорной вероятностью гипотез H _i по наблюдениям (E_j,..., E_k). Эти вероятности дают сравнительное ранжирование всех возможных гипотез, то есть гипотез с ненулевыми апостериорными вероятностями. Результатом вывода ЭС является выбор гипотезы с наибольшей вероятностью.

Однако, приведённая выше формула Байеса ограничена в том, что каждое свидетельство влияет только на одну гипотезу. Можно обобщить это выражение на случай множественных гипотез (H₁,..., H_m) и множественных свидетельств (E₁,..., E_n). Вероятности каждой из гипотез при условии возникновения некоторого конкретного свидетельства E можно определить из выражения:

.

а в случае множественных свидетельств:

.

К сожалению данное выражение имеет ряд недостатков. Так, знаменатель требует от нас знания условных вероятностей всех возможных комбинаций свидетельств и гипотез, что делает правило Байеса малопригодным для ряда приложений. Однако в тех случаях когда возможно предположить условную независимость свидетельств, правило Байеса можно привести к более простому виду:

.

Вместе с тем предположения о независимости событий в ряде случаев подавляют точности суждений и свидетельств в ЭС.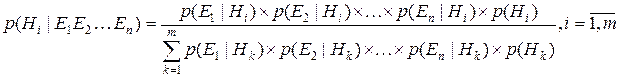