Распространение вероятностей в ЭС
Вероятности событий распространяются по БЗ экспертной системы на основе правила Байеса для вычисления всех апостериорных вероятностей гипотез при условии наблюдаемых свидетельств. Эти апостериорные вероятности дают ранжированную информацию о потенциально истинной гипотезе. Рассмотрим пример, иллюстрирующий этот процесс. Пример. Предположим, что в некоторой БЗ имеется всего три взаимно независимых гипотезы: H1, H2, H3, которые имеют априорные вероятности: p(H1), p(H2), p(H3), соответственно. Правила БЗ содержат два условно независимых свидетельства, которые поддерживают исходные гипотезы в различной степени. Априорные и условные вероятности всех гипотез и свидетельств этого примера имеют следующие значения:
При этом исходные гипотезы характеризуют событие, связанное с определением надежности некоторой фирмы: H1 - “средняя надежность фирмы”, H2 - “высокая надежность фирмы”, H3 - “низкая надежность фирмы”. Событиями, являющимися условно независимыми свидетельствами, поддерживающими исходные гипотезы являются: Е1 – “наличие прибыли у фирмы” и Е2 – “своевременный расчет с бюджетом”. В процессе сбора фактов вероятности гипотез будут повышаться, если факты поддерживают их или уменьшаться, если опровергают их. Предположим, что мы имеем только одно свидетельство E1 (то есть с вероятностью единица наступил факт E1). Наблюдая E1 мы вычисляем апостериорные вероятности для гипотез согласно формуле Байеса для одного свидетельства:
Таким образом
После того как E1 произошло доверие к гипотезам H1 и H3 понизилось, в то время как доверие к H2 возросло. В тех случаях, когда имеются факты, подтверждающие как событие E1, так и событие E2, то апостериорные вероятности исходных гипотез также могут быть вычислены по правилу Байеса:
Так как события E1 и E2 условно независимые при данных гипотезах Hi, то формулу Байеса можно переписать в виде:
Откуда
Хотя исходным ранжированием было H1, H2,и H3, только H1 и H2 остались после получения свидетельств E1 и E2. При этом H1,менее вероятно, чем H2. На этом примере мы рассмотрели процесс распространения вероятностей по элементам ЭС при поступлении в неё тех или иных свидетельств.
|

 p() i
p() i
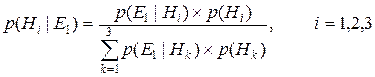 .
. ,
,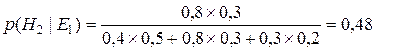 ,
,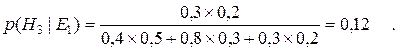
 .
.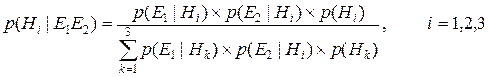 .
.



