Байесовское оценивание.
Перед тем, как ввести теорему Байеса рассмотрим некоторые фундаментальные понятия теории вероятностей. Пусть А некоторое событие реального мира. Совокупность всех элементарных событий называется выборочным пространством или пространство событий (W). Вероятность события А, обозначается р(А) и каждая вероятностная функция р должна удовлетворять трем аксиомам: 1. Вероятность любого события А является неотрицательной, т.е.
2. Вероятность всех событий выборочного пространства равна 1, т.е.
3. Если k событий А1, А2, …, Аk являются взаимно независимыми (т.е. не могут подойти одновременно), то вероятность, по крайней мере, одного из этих событий равна сумме отдельных вероятностей, или
Аксиомы 1 и 2 можно объединить, что дает
Это утверждение показывает, что вероятность любого события находится между 0 и 1. По определению, когда р(А) = 0, то событие А никогда не произойдет. В том случае и когда р(А) = 1, то событие А должно произойти обязательно. Дополнение к А, обозначаемое (A), содержит совокупность всех событий в W за исключением А. Т.к. А и A являются взаимонезависимыми (т.е. А È A= W), то из аксиомы 3 следует р(А) + р(A) = р(А È A) = р( W ) = 1. Переписывая это равенство в виде р(A) = 1 – р(А), мы получает путь для получения р(A) из р(А). Предположим теперь, что В Î W некоторое другое событие. Тогда вероятность того, что произойдет А при условии, что произошло В записывается в виде р(А | B) и называется условной вероятностью события А при заданном событии В. Вероятность того, что оба события А и В произойдут р(А Ç В ) называется совместной вероятностью событий А и В. Условная вероятность р(А|B) равна отношению совместной вероятности р(А Ç В) к вероятности события В, при условии, что она не равна 0, т. е.
Аналогично условная вероятность события В при условии А, обозначаемая р(В|А) равна:
и таким образом
Так, как совместная вероятность коммутативна (т.е. от перестановки мест сумма не меняется), то
Подставляя это равенство в ранее полученное выражение для условной вероятности р(А| В) получим правило Байеса
В ряде случае наше знание того, что произошло событие В, не влияет на вероятность события А (или наоборот А на В). Другими словами, вероятность события А не зависит от того, что произошло или нет событие В, так что р(А | В) = р(А) и р(В | А) = р(В). В этом случае говорят, что события А и В являются независимыми.
|

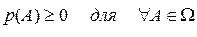
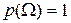 .
.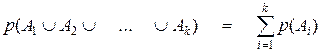
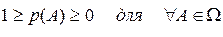 .
.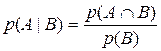
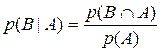
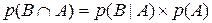 .
.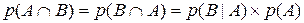 .
.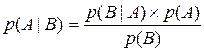 .
.


