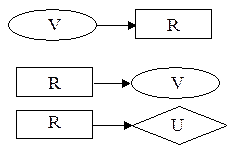Назначение и основные компоненты диаграмм влияния

Диаграммы влияния используются для принятия решений. Фактически диаграммы влияния – это байесовские сети доверия расширенные понятиями пользы (utility) и решения (decisions). Если байесовские сети доверия содержали только один тип вершин, которые мы назовём вершинами шансов, и которые соответствовали состоянию случайных переменных, то в диаграммах влияния используются ещё, как минимум, два типа вершин: вершины решения, обозначаемые в диаграммах влияния прямоугольниками и вершины пользы, обозначаемые в диаграммах влияния в виде ромба.

Вершины решения, а точнее сказать указания, содержащиеся в них, определяют временное старшинство:

· стрелка от случайной переменной (вершины шансов) к переменной решения (вершине решения) указывает, что значение случайной переменной известно на момент принятия решения;

· стрелка от переменной решения к какой-либо другой переменной указывает время, упорядоченное решением.

При этом сеть должна оставаться ациклической и должен существовать непосредственный путь, содержащий все вершины решения в сети.

В процессе принятия решения важно не просто найти решение, а найти решение наилучшее в каком-то смысле. С этой целью в диаграммах влияния «вершины пользы» связываются с состоянием сети.

Каждая вершина пользы (полезности) содержит функцию полезности, которая связывает каждую конфигурацию состояния её родителей с полезностью. Вершины полезности не имеют наследников (а, следовательно, стрелка может быть направлена только к ним), т.е.

Принимая решение мы исходим вероятности конфигурации сети. Поэтому можно вычислить ожидаемую полезность каждой альтернативы и выбрать альтернативу с наибольшей ожидаемой полезностью. Это принцип максимальной ожидаемой полезности. Диаграмма влияния может содержать несколько вершин полезности. При этом общая функция полезности представляет собой сумму всех локальных функций полезности.

Процесс принятия решения с использованием диаграмм влияния будет осуществляться в следующем порядке:

· после наблюдения значений переменных, которые являются родителями первой вершины решения мы хотим знать максимальную полезность для альтернатив;

· ЭС вычислит эти полезности в предположении, что все будущие решения будут сделаны оптимально, используя все имеющиеся свидетельства в момент каждого решения.